
2.求离散型随机变量的期望与方差,首先应明确随机变量的分布列,若分布列中的概率值是待定常数,应先求出这些待定常数后,再求其期望与方差.
1.离散型随机变量的期望和方差都是随机变量的重要的特征数,期望反映了随机变量的平均值,方差反映了随机变量取值的稳定与波动、集中与离散的程度.
9.将数字1,2,3,4任意排成一列,如果数字k恰好出现在第k个位置上,则称之为一个巧合,求巧合数的数学期望.
解:设ξ为巧合数,则P(ξ=0)=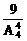 =
=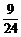 ,P(ξ=1)=
,P(ξ=1)=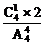 =
=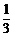 ,P(ξ=2)=
,P(ξ=2)=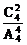 =
=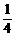 ,P(ξ=3)=0,P(ξ=4)=
,P(ξ=3)=0,P(ξ=4)=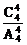 =
=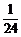 ,
,
所以Eξ=0×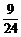 +1×
+1×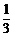 +2×
+2×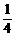 +3×0+4×
+3×0+4×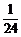 =1.
=1.
所以巧合数的期望为1.
●思悟小结
8.证明:事件在一次实验中发生的次数的方差不超过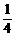 .
.
证明:设事件在一次试验中发生的次数为ξ,ξ的可能取值为0或1,又设事件在一次试验中发生的概率为p,则P(ξ=0)=1-p,P(ξ=1)=p,Eξ=0×(1-p)+1×p=p,Dξ=(1-p)·(0-p)2+p(1-p)2=p(1-p)≤(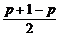 )2=
)2=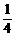 .
.
所以事件在一次试验中发生的次数的方差不超过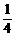 .
.
探究创新
7.一台设备由三大部件组成,在设备运转中,各部件需要调整的概率相应为0.10,0.20和0.30.假设各部件的状态相互独立,以ξ表示同时需要调整的部件数,试求ξ的数学期望Eξ和方差Dξ.
解:设Ai={部件i需要调整}(i=1,2,3),则P(A1)=0.1,P(A2)=0.2,P(A3)=0.3.
由题意,ξ有四个可能值0,1,2,3.由于A1,A2,A3相互独立,可见
P(ξ=0)=P(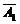
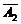
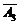 )=0.9×0.8×0.7=0.504;
)=0.9×0.8×0.7=0.504;
P(ξ=1)=P(A1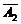
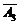 )+P(
)+P(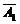 A2
A2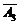 )+P(
)+P(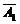
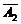 A3)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
A3)=0.1×0.8×0.7+0.9×0.2×0.7+0.9×0.8×0.3=0.398;
P(ξ=2)=P(A1A2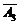 )+P(A1
)+P(A1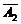 A3)+P(
A3)+P(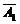 A2A3)=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092;
A2A3)=0.1×0.2×0.7+0.1×0.8×0.3+0.9×0.2×0.3=0.092;
P(ξ=3)=P(A1A2A3)=0.1×0.2×0.3=0.006.
∴Eξ=1×0.398+2×0.092+3×0.006=0.6,
Dξ=Eξ2-(Eξ)2=1×0.398+4×0.092+9×0.006-0.62=0.82-0.36=0.46.
6.袋中有4只红球,3只黑球,今从袋中随机取出4只球.设取到一只红球得2分,取到一只黑球得1分,试求得分ξ的概率分布和数学期望.
解:直接考虑得分的话,情况较复杂,可以考虑取出的4只球颜色的分布情况:
4红得8分,3红1黑得7分,2红2黑得6分,1红3黑得5分,故P(ξ=5)=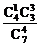 =
=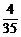 ,
,
P(ξ=6)=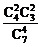 =
=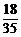 ,P(ξ=7)=
,P(ξ=7)=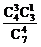 =
=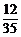 ,
,
P(ξ=8)=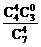 =
=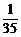 ,Eξ=5×
,Eξ=5×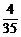 +6×
+6×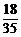 +7×
+7×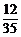 +8×
+8×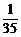 =
=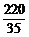 =
=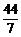 .
.
培养能力
5.一次单元测试由50个选择题构成,每个选择题有4个选项,其中恰有1个是正确答案.每题选择正确得2分,不选或错选得0分,满分是100分.学生甲选对任一题的概率为0.8,求他在这次测试中成绩的期望和标准差.
解:设学生甲答对题数为ξ,成绩为η,则ξ-B(50,0.8),η=2ξ,故成绩的期望为Eη=E(2ξ)=2Eξ=2×50×0.8=80(分);
成绩的标准差为ση=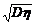 =
=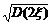 =
=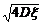 =2
=2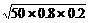 =4
=4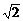 ≈5.7(分).
≈5.7(分).
4.甲从学校乘车回家,途中有3个交通岗,假设在各交通岗遇红灯的事件是相互独立的,并且概率都是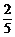 ,则甲回家途中遇红灯次数的期望为________.
,则甲回家途中遇红灯次数的期望为________.
解析:设甲在途中遇红灯次数为ξ,
则ξ-B(3,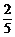 ),
),
所以Eξ=3×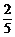 =1.2.
=1.2.
答案:1.2
3.设一次试验成功的概率为p,进行100次独立重复试验,当p=________时,成功次数的标准差的值最大,其最大值为________.
解析:Dξ=npq≤n(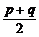 )2=
)2=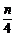 ,等号在p=q=
,等号在p=q=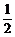 时成立,此时,Dξ=25,σξ=5.
时成立,此时,Dξ=25,σξ=5.
答案: 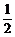 5
5
2.一射手对靶射击,直到第一次命中为止每次命中的概率为0.6,现有4颗子弹,命中后的剩余子弹数目ξ的期望为
A.2.44 B.3.376 C.2.376 D.2.4
解析:ξ=0,1,2,3,此时P(ξ=0)=0.43,P(ξ=1)=0.6×0.42,P(ξ=2)=0.6×0.4,P(ξ=3)=0.6,Eξ=2.376.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com