
4.(2004年北京东城区二模题)已知sinα+cosα=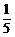 ,那么角α是第_______象限的角.
,那么角α是第_______象限的角.
解析:两边平方得1+2sinαcosα=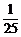 ,
,
∴sinαcosα=-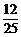 <0.
<0.
∴α是第二或第四象限角.
答案:第二或第四
3.已知tan110°=a,则tan50°=_________.
解析:tan50°=tan(110°-60°)=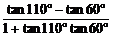 =
=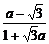 .
.
答案: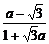
2.设α、β是第二象限的角,且sinα<sinβ,则下列不等式能成立的是
A.cosα<cosβ B.tanα<tanβ
C.cotα>cotβ D.secα<secβ
解析:A与D互斥,B与C等价,则只要判断A与D对错即可.利用单位圆或特殊值法,易知选A.
答案:A
1.角α的终边过点P(-8m,-6cos60°)且cosα=-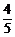 ,则m的值是
,则m的值是
A.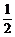 B.-
B.-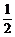 C.-
C.-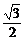 D.
D.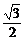
解析:P(-8m,-3),cosα=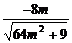 =-
=-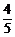 .
.
∴m=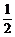 或m=-
或m=-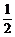 (舍去).
(舍去).
答案:A
5.化简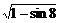 =_________.
=_________.
解析: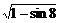 =
=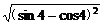 =|sin4-cos4|=sin4-cos4.
=|sin4-cos4|=sin4-cos4.
答案:sin4-cos4
●典例剖析
[例1] (1)若θ是第二象限的角,则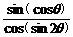 的符号是什么?
的符号是什么?
(2)π<α+β<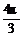 ,-π<α-β<-
,-π<α-β<-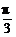 ,求2α-β的范围.
,求2α-β的范围.
剖析:(1)确定符号,关键是确定每个因式的符号,而要分析每个因式的符号,则关键看角所在象限.
(2)可以把α+β与α-β看成两个变量(整体思想),然后把2α-β用这两个变量表示出来即可.
解:(1)∵2kπ+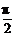 <θ<2kπ+π(k∈Z),
<θ<2kπ+π(k∈Z),
∴-1<cosθ<0,4kπ+π<2θ<4kπ+2π,-1<sin2θ<0.
∴sin(cosθ)<0,cos(sin2θ)>0.
∴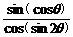 <0.
<0.
(2)设x=α+β,y=α-β,2α-β=mx+ny,
则2α-β=mα+mβ+nα-nβ=(m+n)α+(m-n)β.
∴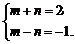 ∴m=
∴m=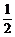 ,n=
,n=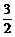 .
.
∴2α-β=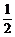 x+
x+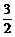 y.
y.
∵π<x<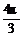 ,-π<y<-
,-π<y<-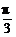 ,
,
∴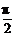 <
<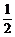 x<
x<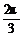 ,-
,- <
<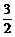 y<-
y<-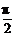 .
.
∴-π<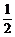 x+
x+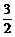 y<
y<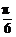 .
.
评述:(1)解此题的常见错误是:
π<α+β<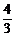 π, ①
π, ①
-π<α-β<-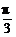 , ②
, ②
①+②得0<2α<π, ③
由②得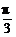 <β-α<π, ④
<β-α<π, ④
①+④得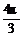 <2β<
<2β<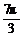 ,∴
,∴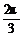 <β<
<β<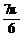 . ⑤
. ⑤
∴-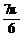 <-β<-
<-β<-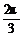 . ⑥
. ⑥
③+⑥得-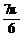 <2α-β<
<2α-β<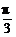 .
.
(2)本题可用线性规划求解,读者不妨一试.
[例2] 已知cosα=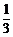 ,且-
,且-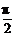 <α<0,
<α<0,
求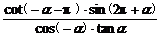 的值.
的值.
剖析:从cosα=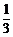 中可推知sinα、cotα的值,再用诱导公式即可求之.
中可推知sinα、cotα的值,再用诱导公式即可求之.
解:∵cosα=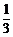 ,且-
,且-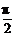 <α<0,
<α<0,
∴sinα=-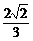 ,cotα=-
,cotα=-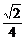 .
.
∴原式=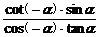 =
=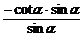 =-cotα=
=-cotα=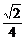 .
.
评述:三角函数式的化简求值是三角函数中的基本问题,也是常考的问题之一.
[例3] 已知sinβ=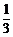 ,sin(α+β)=1,求sin(2α+β)的值.
,sin(α+β)=1,求sin(2α+β)的值.
剖析:由已知sin(α+β)=1,则α+β=2kπ+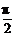 ,再将2α+β改造成2(α+β)-β即可求之.
,再将2α+β改造成2(α+β)-β即可求之.
解:∵sin(α+β)=1,∴α+β=2kπ+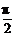 .
.
∴sin(2α+β)=sin[2(α+β)-β]=sinβ=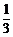 .
.
评述:整体代入是常用的技巧,这里要分析已知和要求的结论之间的角的关系和三角函数名称之间的关系.
●闯关训练
夯实基础
4.若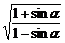 =
=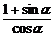 ,则α的取值范围是_______.
,则α的取值范围是_______.
解析:∵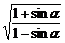 =
=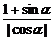 =
=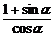 ,
,
∴cosα>0.∴α∈(2kπ-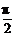 ,2kπ+
,2kπ+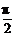 )(k∈Z).
)(k∈Z).
答案:α∈(2kπ-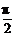 ,2kπ+
,2kπ+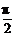 )(k∈Z)
)(k∈Z)
3.α是第二象限角,P(x,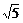 )为其终边上一点且cosα=
)为其终边上一点且cosα=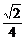 x,则x的值为
x,则x的值为
A.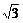 B.±
B.±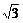 C.-
C.-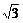 D.-
D.-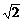
解析:∵cosα=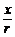 =
=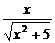 =
=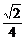 x,
x,
∴x=0(舍去)或x=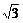 (舍去)或x=-
(舍去)或x=-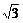 .
.
答案:C
2.设cosα=t,则tan(π-α)等于
A.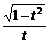 B.-
B.-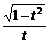 C.±
C.±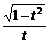 D.±
D.±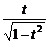
解析:tan(π-α)=-tanα=-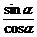 .
.
∵cosα=t,又∵sinα=±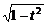 ,
,
∴tan(π-α)=±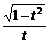 .
.
答案:C
1.已知sin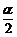 =
=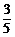 ,cos
,cos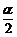 =-
=-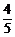 ,那么α的终边在
,那么α的终边在
A.第一象限 B.第三或第四象限
C.第三象限 D.第四象限
解析:sinα=2sin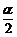 cos
cos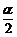 =-
=-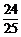 <0,
<0,
cosα=cos2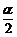 -sin2
-sin2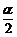 =
=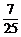 >0,
>0,
∴α终边在第四象限.
答案:D
3.诱导公式
α+2kπ(k∈Z)、-α、π±α、2π-α的三角函数值,等于α的同名函数值,前面加上一个把α看成锐角时原函数值的符号.
另外:sin(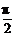 -α)=cosα,cos(
-α)=cosα,cos(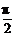 -α)=sinα.
-α)=sinα.
●点击双基
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com