
3.(2004年湖北,理14)将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子内,每个盒内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有_____________种.(以数字作答)
解析:从10个盒中挑3个与球标号不一致,共C 种挑法,每一种3个盒子与球标号全不一致的方法为2种,∴共有2C
种挑法,每一种3个盒子与球标号全不一致的方法为2种,∴共有2C =240种.
=240种.
答案:240
2.(2004年江苏,3)从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有
A.140种 B.120种 C.35种 D.34种
解析:7人中任选4人,共C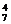 种选法,扣除只有男生的选法C
种选法,扣除只有男生的选法C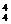 ,就可得有既有男生,又有女生的选法C
,就可得有既有男生,又有女生的选法C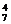 -C
-C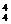 =34.
=34.
答案:D
1.从6双不同颜色的手套中任取4只,其中恰好有一双同色的取法有
A.240种 B.180种 C.120种 D.60种
解析:先从6双手套中任选一双,有C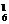 种取法,再从其余手套中任选2只,有C
种取法,再从其余手套中任选2只,有C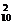 种,其中选一双同色手套的选法为C
种,其中选一双同色手套的选法为C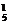 种.故总的选法数为C
种.故总的选法数为C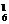 (C
(C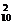 -C
-C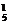 )=240种.
)=240种.
答案:A
2.从一楼到二楼楼梯一共10级,上楼可以一步上一级,也可以一步上两级,规定用8步走完楼梯的方法种数是_____________.
解:设一步一级x步,一步两级y步,则
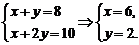
故走完楼梯的方法有C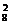 =28种.
=28种.
●闯关训练
夯实基础
1.某城市由n条东西方向的街道和m条南北方向的街道组成一个矩形街道网,如下图所示.要从A处走到B处,使所走的路程最短,有多少种不同的走法?
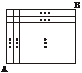
解:将相邻两个交点之间的街道称为一段,那么从A到B需要走(n+m-2)段,而这些段中,必须有东西方向的(n-1)段,其余的为南北方向的(m-1)段,所以共有C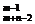 =C
=C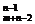 种走法.
种走法.
5.某校准备参加2004年全国高中数学联赛,把10个名额分配给高三年级8个班,每班至少1人,不同的分配方案有_____________种.
解析:把10个名额分成8份,每份至少一个名额即可,用隔板法:C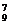 =C
=C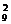 =36.
=36.
答案:36
●典例剖析
[例1] 某外语组有9人,每人至少会英语和日语中的一门,其中7人会英语,3人会日语,从中选取会英语和日语的各一人,有多少种不同的选法?
解:由题意可知,只会英语的有6人,只会日语的有2人,英语和日语都会的有1人.
以只会英语的人数分类,C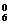 ·C
·C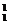 ·C
·C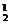 +C
+C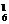 ·C
·C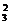 =20.
=20.
[例2] 设集合A={1,2,3,…,10},
(1)设A的3个元素的子集的个数为n,求n的值;
(2)设A的3个元素的子集中,3个元素的和分别为a1,a2,…,an,求a1+a2+a3+…+an的值.
解:(1)A的3元素子集的个数为n=C =120.
=120.
(2)在A的3元素子集中,含数k(1≤k≤10)的集合个数有C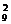 个,因此a1+a2+…+an=
个,因此a1+a2+…+an=
C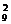 ×(1+2+3+…+10)=1980.
×(1+2+3+…+10)=1980.
评述:在求从n个数中取出m(m≤n)个数的所有组合中各组合中数字的和时,一般先求出含每个数字的组合的个数,含每个数字的个数一般都相等,故每个数字之和与个数之积便是所求结果.
[例3] 从1,2,…,30这30个自然数中,每次取不同的三个数,使这三个数的和是3的倍数的取法有多少种?
解:令A={1,4,7,10,…,28},B={2,5,8,11,…29},C={3,6,9,…,30}组成三类数集,有以下四类符合题意:①A,B,C中各取一个数,有C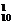 C
C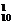 C
C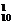 种;②仅在A中取3个数,有C
种;②仅在A中取3个数,有C 种;③仅在B中取3个数,有C
种;③仅在B中取3个数,有C 种;④仅在C中取3个数,有C
种;④仅在C中取3个数,有C 种.故由加法原理得共有C
种.故由加法原理得共有C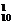 ·C
·C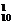 ·C
·C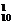 +3C
+3C =1360种.
=1360种.
评述:按元素的性质分类是处理带限制条件的组合问题的常用方法,对于某几个数的和能被某数整除一类的问题,通常是将整数分类,凡余数相同者归同一类.
思考讨论
讨论下面的问题:
用0,1,2,3,4,5这六个数字可以组成没有重复数字的能被25整除的四位数多少个?
提示:能被25整除的数的后两位是25或50,后两位是50的数有A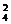 个,后两位是25的数有3×3=9个,所以能被25整除的四位数的个数为A
个,后两位是25的数有3×3=9个,所以能被25整除的四位数的个数为A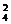 +9=21.
+9=21.
[例4] 如图,从一个3×4的方格中的一个顶点A到对顶顶点B的最短路线有几条?

解:从A到B的最短路线,均需走7步,包括横向的4步和纵向的3步,于是我们只要确定第1,2,…,7步哪些是横向的,哪些是纵向的就可以了,实际只要确定哪几步是横向走.所以每一条从A到B的最短路线对应着从第1,2,…,7步取出4步(横向走)的一个组合,因此从A到B的最短路线共有C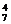 =C
=C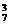 =35条.
=35条.
深化拓展
4.(2003年东北三校模拟题)将一个四棱锥的每个顶点染上一种颜色,并使同一条棱的两端异色.若只有五种颜色可供使用,则不同的染色方法种数为_____________.
解析:设四棱锥为P-ABCD.(1)P:C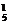 ,A:C
,A:C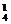 ,B:C
,B:C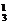 ,C与B同色:1,D:C
,C与B同色:1,D:C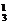 .
.
(2)P:C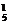 ,A:C
,A:C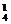 ,B:C
,B:C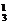 ,C与B不同色C
,C与B不同色C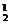 ,D:C
,D:C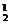 .
.
共有C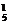 ·C
·C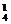 ·C
·C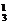 ·1·C
·1·C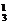 +C
+C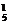 ·C
·C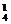 ·C
·C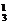 ·C
·C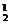 ·C
·C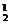 =420.
=420.
答案:420
3.已知{1,2}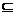 X
X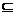 {1,2,3,4,5},满足这个关系式的集合X共有_____________个.
{1,2,3,4,5},满足这个关系式的集合X共有_____________个.
A.2 B.6 C.4 D.8
解析:由题意知集合X中的元素1,2必取,另外可从3,4,5中可以不取,取1个,取2个,取3个,
故有C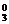 +C
+C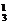 +C
+C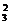 +C
+C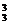 =8(个).
=8(个).
答案:D
2.(2004年北京,理17)从长度分别为1、2、3、4、5的五条线段中,任取三条的不同取法共有n种.在这些取法中,以取出的三条线段为边可组成的钝角三角形的个数为m,则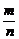 等于
等于
A.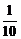 B.
B.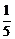 C.
C.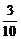 D.
D.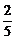
解析:n=C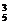 =10,由余弦定理知可组成钝角三角形的有“2、3、4”和“2、4、5”,故m=2.
=10,由余弦定理知可组成钝角三角形的有“2、3、4”和“2、4、5”,故m=2.
∴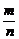 =
=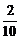 =
=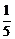 .
.
答案:B
1.从4台甲型电脑和5台乙型电脑中任取3台,其中两种电脑都要取,则不同的取法种数是
A.140 B.84 C.70 D.35
解析:取3台分两类:①2台甲型1台乙型,有C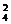 ·C
·C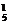 种;
种;
②1台甲型2台乙型,有C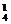 ·C
·C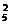 种.
种.
∴C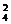 ·C
·C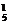 +C
+C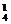 ·C
·C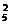 =30+40=70(种).
=30+40=70(种).
答案:C
特别提示
先从甲型、乙型中各抽1台,有C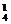 ·C
·C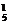 种,再从余下的中选1台,有C
种,再从余下的中选1台,有C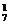 种,
种,
故有C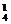 ·C
·C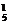 ·C
·C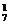 =140(种).解法不正确.
=140(种).解法不正确.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com