1.定义

数列{a_n}从第2项起，每一项与它前一项的比等于同一个常数的数列称作等比数列.常数叫公比.

3.3　 等比数列

●知识梳理

5.在求解数列问题时，要注意函数思想、方程思想、消元及整体消元的方法的应用.

拓展题例

[例1] 已知两个等差数列5，8，11，…和3，7，11，…都有100项，问它们有多少相同的项？并求所有相同项的和.

分析一：两个等差数列的相同的项按原来的先后次序组成一个等差数列，且公差为原来两个公差的最小公倍数.

解法一：设两个数列相同的项按原来的前后次序组成的新数列为{a_n}，则a₁=11.

∵数列5，8，11，…与3，7，11，…公差分别为3与4，

∴{a_n}的公差d=3×4=12，∴a_n=12n－1.

又∵5，8，11，…与3，7，11，…的第100项分别是302与399，∴a_n=12n－1≤302，即n≤25.5.

又n∈N^*，∴两个数列有25个相同的项.

其和S₂₅=11×25+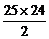×12=3875.

分析二：由条件可知两个等差数列的通项公式，可用不定方程的求解方法来求解.

解法二：设5，8，11，…与3，7，11，…分别为{a_n}与{b_n}，则a_n=3n+2，b_n=4n－1.

设{a_n}中的第n项与{b_n}中的第m项相同，

即3n+2=4m－1，∴n=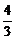m－1.

又m、n∈N^*，∴设m=3r(r∈N^*)，

得n=4r－1.

根据题意得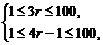

解得1≤r≤25(r∈N^*).

从而有25个相同的项，且公差为12，

其和S₂₅=11×25+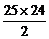×12=3875.

[例2] 设{a_n}为等差数列，S_n为数列{a_n}的前n项和，已知S₇=7，S₁₅=75，T_n为数列{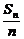}的前n项和，求T_n.

解：设等差数列{a_n}的公差为d，则S_n=na₁+n(n－1)d.

∵S₇=7，S₁₅=75，

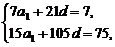∴即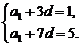

解得a₁=－2，d=1.

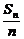∴=a₁+(n－1)d=－2+(n－1)=.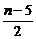

∴－=.

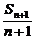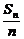∴数列{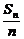}是等差数列，其首项为－2，公差为.

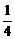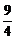∴T_n=n²－n.

4.等差数列的性质在求解中有着十分重要的作用，应熟练掌握、灵活运用.

3.已知三个或四个数成等差数列这类问题，要善于设元，目的仍在于减少运算量，如三个数成等差数列时，除了设a，a+d，a+2d外，还可设a－d，a，a+d；四个数成等差数列时，可设为a－3d，a－d，a+d，a+3d.

2.由五个量a₁，d，n，a_n，S_n中的三个量可求出其余两个量，要求选用公式要恰当，即善于减少运算量，达到快速、准确的目的.

1.在熟练应用基本公式的同时，还要会用变通的公式，如在等差数列中，a_m=a_n+(m－n)d.

5.复习时，要注意以下几点：

(1)深刻理解等差数列的定义及等价形式，灵活运用等差数列的性质.

(2)注意方程思想、整体思想、分类讨论思想、数形结合思想的运用.

●教师下载中心

教学点睛

本节教学时应注意以下几个问题：

4.等差数列{a_n}中，当a₁＜0，d＞0时，数列{a_n}为递增数列，S_n有最小值；当a₁＞0，d＜0时，数列{a_n}为递减数列，S_n有最大值；当d=0时，{a_n}为常数列.

3.证明数列{a_n}是等差数列的两种基本方法是：

(1)利用定义，证明a_n－a_n－1(n≥2)为常数；

(2)利用等差中项，即证明2a_n=a_n－1+a_n+1(n≥2).