
3.函数的最大值与最小值
(1)设y=f(x)是定义在区间[a,b]上的函数,y=f(x)在(a,b)内有导数,求函数y=f(x)在[a,b]上的最大值与最小值,可分两步进行.
①求y=f(x)在(a,b)内的极值.
②将y=f(x)在各极值点的极值与f(a)、f(b)比较,其中最大的一个为最大值,最小的一个为最小值.
(2)若函数f(x)在[a,b]上单调增加,则f(a)为函数的最小值,f(b)为函数的最大值;若函数f(a)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.
特别提示
我们把使导函数f′(x)取值为0的点称为函数f(x)的驻点,那么
(1)可导函数的极值点一定是它的驻点,注意这句话中的“可导”两字是必不可少的.例如函数y=|x|在点x=0处有极小值f(0)=0,可是我们在前面已说明过,f′(0)根本不存在,所以点x=0不是f(x)的驻点.
(2)可导函数的驻点可能是极值点,也可能不是极值点.例如函数f(x)=x3的导数是 f′(x)=3x2,在点x=0处有f′(0)=0,即点x=0是f(x)=x3的驻点,但从f(x)在(-∞, +∞)上为增函数可知,点x=0不是f(x)的极值点.
●点击双基
2.可导函数的极值
(1)极值的概念
设函数f(x)在点x 0附近有定义,且若对x0附近所有的点都有f(x)<f(x0)(或f(x)>f(x0)),则称f(x0)为函数的一个极大(小)值,称x0为极大(小)值点.
(2)求可导函数f(x)极值的步骤.
①求导数f′(x).
②求方程f′(x)=0的根.
③检验f′(x)在方程f′(x)=0的根的左右的符号,如果在根的左侧附近为正,右侧附近为负,那么函数y=f(x)在这个根处取得极大值;如果在根的左侧附近为负,右侧附近为正,那么函数y=f(x)在这个根处取得极小值.
1.函数的单调性
(1)设函数y=f(x)在某个区间内可导,若f′(x)>0,则f(x)为增函数;若f′(x)<0,则f(x)为减 函数.
(2)求可导函数单调区间的一般步骤和方法.
①确定函数f(x)的定义区间.
②求f′(x),令f′(x)=0,解此方程,求出它在定义区间内的一切实根.
③把函数f(x)的间断点(即包括f(x)的无定义点)的横坐标和上面的各实根按由小到大的顺序排列起来,然后用这些点把函数f(x)的定义区间分成若干个小区间.
④确定f′(x)在各小开区间内的符号,根据f′(x)的符号判定函数f(x)在每个相应小开区间内的增减性.
14.2 导数的应用
●知识梳理
2.可补充导数的另一种定义形式:f′(x0)=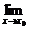
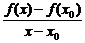 .
.
拓展题例
[例题] 讨论函数f(x)=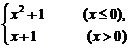 在x=0处的可导性.
在x=0处的可导性.
解:函数f(x)在x=0处是否可导,即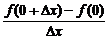 当Δx→0时的极限是否存在.
当Δx→0时的极限是否存在.
∵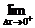
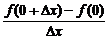
=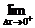
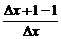 =1,
=1,
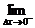
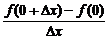
=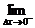
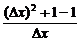 =0,
=0,
又∵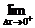
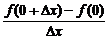 ≠
≠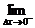
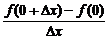 ,
,
∴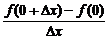 当Δx→0时的极限不存在,因此f(x)在x=0处不可导.
当Δx→0时的极限不存在,因此f(x)在x=0处不可导.
1.在该节教学中要重视对导数的概念、导数的几何意义的理解,注重对导数基本公式的熟练运用.
3.本单元重点体现了极限思想、函数思想及等价转化的思想,在学习过程中应用心体会.
●教师下载中心
教学点睛
2.求复合函数的导数的方法步骤:
(1)分清复合函数的复合关系,选好中间变量.
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数.
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数.
1.求函数y=f(x)在点x0处的导数通常有以下两种方法:
(1)导数的定义,即求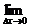
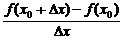 的值.
的值.
(2)利用导函数的函数值,即先求函数f(x)在开区间(a,b)内的导函数f′(x),再将x0(x0∈(a,b))代入导函数f(x),得函数值f′(x0).
9.利用导数求和:
(1)Sn=1+2x+3x2+…+nxn-1(x≠0,n∈N *).
(2)Sn=C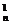 +2C
+2C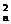 +3C
+3C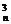 +…+nC
+…+nC (n∈N *).
(n∈N *).
解:(1)当x=1时,Sn=1+2+3+…+n=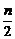 (n+1),
(n+1),
当x≠1时,∵x+x2+x3+…+xn=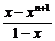 ,
,
两边对x求导,得Sn=1+2x+3x2+…+nxn-1=(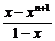 )=
)=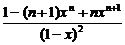 .
.
(2)∵(1+x)n=1+C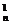 x+C
x+C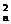 x2+…+C
x2+…+C xn,
xn,
两边对x求导,得n(1+x)n-1=C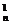 +2C
+2C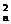 x+3C
x+3C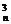 x2+…+nC
x2+…+nC x n-1.
x n-1.
令x=1,得n·2n-1=C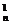 +2C
+2C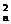 +3C
+3C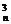 +…+nC
+…+nC ,
,
即Sn=C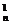 +2C
+2C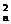 +3C
+3C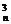 +…+nC
+…+nC =n·2n-1.
=n·2n-1.
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com