
1.理解集合、子集、补集、交集、并集的概念;了解属于、包含、相等关系的意义.
3.求可导函数f(x)的最值的方法:
(1)求f(x)在给定区间内的极值;
(2)将f(x)的各极值与端点值比较,其中最大的一个是最大值,最小的一个是最小值.
拓展题例
[例1] 若函数f(x)=ax3-x2+x-5在(-∞,+∞)上单调递增,求a的取值范围.
解:  (x)=3ax2-2x+1>0恒成立.
(x)=3ax2-2x+1>0恒成立.
∴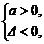 即
即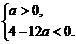
∴a> .
.
当a= 时,f(x)在(-∞,+∞)上单调递增.
时,f(x)在(-∞,+∞)上单调递增.
∴a≥ .
.
[例2] 求证:x>1时,2x3>x2+1.
证明:令f(x)=2x3-x2-1,则 (x)=6x2-2x=2x(3x-1).
(x)=6x2-2x=2x(3x-1).
当x>1时, (x)>0恒成立.
(x)>0恒成立.
∴f(x)在(1,+∞)上单调递增.
又∵f(1)=0,
∴f(x)在(1,+∞)上恒大于零,即当x>1时,2x3>x2+1.
2.求可导函数f(x)的极值的步骤如下:
(1)求f(x)的定义域,求 (x);
(x);
(2)由 (x)=0,求其稳定点;
(x)=0,求其稳定点;
(3)检查 (x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取极大值;如果左负右正,那么f(x)在这个根处取极小值;如果左右同号,那么f(x)在这个根处不取极值.
(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取极大值;如果左负右正,那么f(x)在这个根处取极小值;如果左右同号,那么f(x)在这个根处不取极值.
1.可导函数f(x)在极值点的导数为0,但是导数为0的点不一定是极值点.如果f(x)在x0处连续,在x0两侧的导数异号,那么点x0是函数f(x)的极值点.
2.f(x)是增函数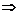
 (x)≥0(f(x)为减函数
(x)≥0(f(x)为减函数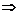
 (x)≤0).
(x)≤0).
●教师下载中心
教学点睛
1. (x)>0
(x)>0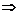 f(x)为增函数(
f(x)为增函数( (x)<0
(x)<0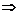 f(x)为减函数).
f(x)为减函数).
10.有点难度哟!
证明方程x3-3x+c=0在[0,1]上至多有一实根.
证明:设f(x)=x3-3x+c,则 (x)=3x2-3=3(x2-1).
(x)=3x2-3=3(x2-1).
当x∈(0,1)时, (x)<0恒成立.
(x)<0恒成立.
∴f(x)在(0,1)上单调递减.
∴f(x)的图象与x轴最多有一个交点.
因此方程x3-3x+c=0在[0,1)上至多有一实根.
●思悟小结
9.已知函数f(x)=2ax-x3,a>0,若f(x)在x∈(0,1]上是增函数,求a的取值范围.
解: (x)=2a-3x2在(0,1]上恒为正,
(x)=2a-3x2在(0,1]上恒为正,
∴2a>3x2,即a>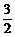 x2.
x2.
∵x∈(0,1],
∴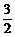 x2∈(0,
x2∈(0,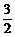 ].
].
∴a>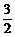 .当a=
.当a=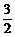 时也成立.∴a≥
时也成立.∴a≥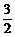 .
.
探究创新
8.已知函数f(x)=ax4+bx2+c的图象经过点(0,1),且在x=1处的切线方程是y=x-2.
(1)求y=f(x)的解析式;
(2)求y=f(x)的单调递增区间.
解:(1)由题意知f(0)=1, (1)=1,f(1)=-1.
(1)=1,f(1)=-1.
∴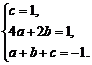
∴c=1,a=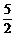 ,b=-
,b=-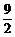 ,
,
f(x)=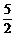 x4-
x4-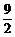 x2+1.
x2+1.
(2)∵ (x)=10x3-9x,
(x)=10x3-9x,
由10x3-9x>0,得x∈(-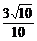 ,0)∪(
,0)∪(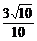 ,+∞),
,+∞),
则f(x)的单调递增区间为(-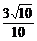 ,0)和(
,0)和(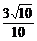 ,+∞).
,+∞).
7.已知函数f(x)=x3-ax-1.
(1)若f(x)在实数集R上单调递增,求实数a的取值范围;
(2)是否存在实数a,使f(x)在(-1,1)上单调递减?若存在,求出a的取值范围,若不存在,请说明理由;
(3)证明f(x)=x3-ax-1的图象不可能总在直线y=a的上方.
解: (x)=3x2-a,(1)3x2-a>0在R上恒成立,∴a<0.
(x)=3x2-a,(1)3x2-a>0在R上恒成立,∴a<0.
又a=0时,f(x)=x3-1在R上单调递增,∴a≤0.
(2)3x2-a<0在(-1,1)上恒成立,即a>3x2在(-1,1)上恒成立,即a>3.
又a=3,f(x)=x3-3x-1, (x)=3(x2-1)在(-1,1)上,
(x)=3(x2-1)在(-1,1)上, (x)<0恒成立,即f(x)在(-1,1)上单调递减,∴a≥3.
(x)<0恒成立,即f(x)在(-1,1)上单调递减,∴a≥3.
(3)当x=-1时,f(-1)=a-2<a,因此f(x)的图象不可能总在直线y=a的上方.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com