
1.设服从二项分布B(n,p)的随机变量ξ的期望和方差分别是2.4与1.44,则二项分布的参数n、p的值为
A.n=4,p=0.6 B.n=6,p=0.4
C.n=8,p=0.3 D.n=24,p=0.1
解析:由Eξ=2.4=np,Dξ=1.44=np(1-p),可得
1-p=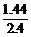 =0.6,p=0.4,n=
=0.6,p=0.4,n= =6.
=6.
答案:B
5.有两台自动包装机甲与乙,包装重量分别为随机变量ξ1、ξ2,已知Eξ1=Eξ2,Dξ1>Dξ2,则自动包装机________的质量较好.
解析:Eξ1=Eξ2说明甲、乙两机包装的重量的平均水平一样.Dξ1>Dξ2说明甲机包装重量的差别大,不稳定.∴乙机质量好.
答案:乙
●典例剖析
[例1] 设ξ是一个离散型随机变量,其分布列如下表,试求Eξ、Dξ.
|
ξ |
-1 |
0 |
1 |
|
P |
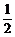 |
1-2q |
q2 |
剖析:应先按分布列的性质,求出q的值后,再计算出Eξ、Dξ.
解:因为随机变量的概率非负且随机变量取遍所有可能值时相应的概率之和等于1,所以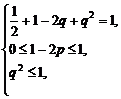 解得q=1-
解得q=1-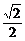 .
.
于是,ξ的分布列为
|
ξ |
-1 |
0 |
1 |
|
P |
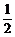 |
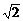 -1 -1 |
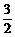 - -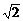 |
所以Eξ=(-1)×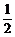 +0×(
+0×(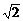 -1)+1×(
-1)+1×(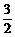 -
-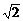 )=1-
)=1-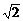 ,
,
Dξ=[-1-(1-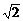 )]2×
)]2×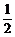 +(1-
+(1-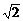 )2×(
)2×(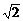 -1)+[1-(1-
-1)+[1-(1-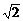 )]2×(
)]2×(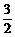 -
-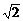 )=
)=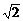 -1.
-1.
评述:解答本题时,应防止机械地套用期望和方差的计算公式,出现以下误解:Eξ=(-1)×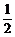 +0×(1-2q)+1×q2=q2-
+0×(1-2q)+1×q2=q2-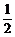 .
.
拓展提高
既要会由分布列求Eξ、Dξ,也要会由Eξ、Dξ求分布列,进行逆向思维.如:若ξ是离散型随机变量,P(ξ=x1)=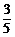 ,P(ξ=x2)=
,P(ξ=x2)=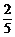 ,且x1<x2,又知Eξ=
,且x1<x2,又知Eξ=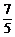 ,Dξ=
,Dξ= .求ξ的分布列.
.求ξ的分布列.
解:依题意ξ只取2个值x1与x2,于是有
Eξ=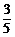 x1+
x1+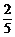 x2=
x2=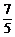 ,
,
Dξ=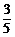 x12+
x12+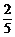 x22-Eξ2=
x22-Eξ2= .
.
从而得方程组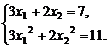
解之得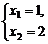 或
或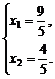
而x1<x2,∴x1=1,x2=2.
∴ξ的分布列为
|
ξ |
1 |
2 |
|
P |
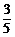 |
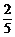 |
[例2] 人寿保险中(某一年龄段),在一年的保险期内,每个被保险人需交纳保费a元,被保险人意外死亡则保险公司赔付3万元,出现非意外死亡则赔付1万元.经统计此年龄段一年内意外死亡的概率是p1,非意外死亡的概率为p2,则a需满足什么条件,保险公司才可能盈利?
剖析:要使保险公司能盈利,需盈利数ξ的期望值大于0,故需求Eξ.
解:设ξ为盈利数,其概率分布为
|
ξ |
a |
a-30000 |
a-10000 |
|
P |
1-p1-p2 |
p1 |
p2 |
且Eξ=a(1-p1-p2)+(a-30000)p1+(a-10000)p2=a-30000p1-10000p2.
要盈利,至少需使ξ的数学期望大于零,故a>30000p1+10000p2.
评述:离散型随机变量的期望表征了随机变量取值的平均值.
思考讨论
本题中Dξ有什么实际意义?
[例3] 把4个球随机地投入4个盒子中去,设ξ表示空盒子的个数,求Eξ、Dξ.
剖析:每个球投入到每个盒子的可能性是相等的.总的投球方法数为44,空盒子的个数可能为0个,此时投球方法数为A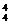 =4!,∴P(ξ=0)=
=4!,∴P(ξ=0)=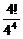 =
=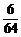 ;空盒子的个数为1时,此时投球方法数为C
;空盒子的个数为1时,此时投球方法数为C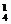 C
C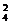 A
A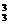 ,
,
∴P(ξ=1)=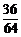 .
.
同样可分析P(ξ=2),P(ξ=3).
解:ξ的所有可能取值为0,1,2,3.
P(ξ=0)=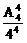 =
=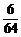 ,P(ξ=1)=
,P(ξ=1)=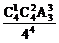 =
=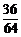 ,P(ξ=2)=
,P(ξ=2)=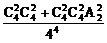 =
=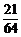 ,P(ξ=3)=
,P(ξ=3)=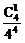 =
=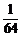 .
.
∴ξ的分布列为
|
ξ |
0 |
1 |
2 |
3 |
|
P |
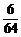 |
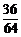 |
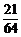 |
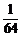 |
∴Eξ=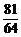 ,Dξ=
,Dξ=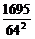 .
.
评述:本题的关键是正确理解ξ的意义,写出ξ的分布列.
特别提示
求投球的方法数时,要把每个球看成不一样的.ξ=2时,此时有两种情况:①有2个空盒子,每个盒子投2个球;②1个盒子投3个球,另1个盒子投1个球.
●闯关训练
夯实基础
4.一牧场有10头牛,因误食含有病毒的饲料而被感染,已知该病的发病率为0.02.设发病的牛的头数为ξ,则Dξ等于
A.0.2 B.0.8 C.0.196 D.0.804
解析:Dξ=10×0.02×0.98=0.196.
答案:C
3.已知ξ-B(n,p),且Eξ=7,Dξ=6,则p等于
A.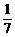 B.
B.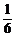 C.
C.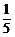 D.
D.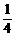
解析:Eξ=np=7,Dξ=np(1-p)=6,所以p=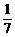 .
.
答案:A
2.设导弹发射的事故率为0.01,若发射10次,其出事故的次数为ξ,则下列结论正确的是
A.Eξ=0.1 B.Dξ=0.1
C.P(ξ=k)=0.01k·0.9910-k D.P(ξ=k)=C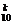 ·0.99k·0.0110-k
·0.99k·0.0110-k
解析:ξ-B(n,p),Eξ=10×0.01=0.1.
答案:A
1.设投掷1颗骰子的点数为ξ,则
A.Eξ=3.5,Dξ=3.52 B.Eξ=3.5,Dξ=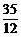
C.Eξ=3.5,Dξ=3.5 D.Eξ=3.5,Dξ=
解析:ξ可以取1,2,3,4,5,6.
P(ξ=1)=P(ξ=2)=P(ξ=3)=P(ξ=4)=P(ξ=5)=P(ξ=6)=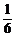 ,
,
∴Eξ=1×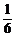 +2×
+2×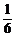 +3×
+3×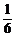 +4×
+4×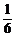 +5×
+5×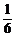 +6×
+6×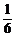 =3.5,
=3.5,
Dξ=[(1-3.5)2+(2-3.5)2+(3-3.5)2+(4-3.5)2+(5-3.5)2+(6-3.5)2]×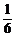 =
=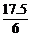 =
=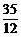 .
.
答案:B
3.性质:(1)E(aξ+b)=aEξ+b,D(aξ+b)=a2Dξ(a、b为常数).
(2)若ξ-B(n,p),则Eξ=np,Dξ=npq(q=1-p).
●点击双基
2.方差:称Dξ=∑(xi-Eξ)2pi为随机变量ξ的均方差,简称方差.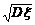 叫标准差,反映了ξ的离散程度.
叫标准差,反映了ξ的离散程度.
1.期望:若离散型随机变量ξ,当ξ=xi的概率为P(ξ=xi)=Pi(i=1,2,…,n,…),则称Eξ=∑xi pi为ξ的数学期望,反映了ξ的平均值.
12.2 离散型随机变量的期望值和方差
●知识梳理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com