
1.要搞清组合与排列的区别与联系:组合与顺序无关,排列与顺序有关;排列可以分成先选取(组合)后排列两个步骤进行.
4.各种与元素的位置、顺序无关的组合问题,常见的有选派问题、抽样问题、图形问题、集合问题、分组问题,解答组合问题的关键是用好组合的定义和两个基本原理,只选不排,合理分类、分步.
●教师下载中心
教学点睛
3.解组合应用题时,应注意至少、至多、最多、恰好等词的含义.
2.解受条件限制的组合题,通常有直接法(合理分类)和间接法(排除法).
1.组合数公式有连乘和阶乘形式,阶乘形式一般用于证明和计算,组合数的性质常用于证明等式及合并组合数简化计算.
8.有点难度哟!
从1到100这100个正整数中,每次取出2个数使它们的和大于100,共有多少种取法?
解:(1)若取出的2个数都大于50,则有C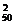 种.
种.
(2)若取出的2个数有一个小于或等于50,
当取1时,另1个只能取100,有C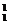 种取法;
种取法;
当取2时,另1个只能取100或99,有C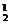 种取法;
种取法;
……
当取50时,另1个数只能取100,99,98,…,51中的一个,有C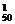 种取法,所以共有1+2+3+…+50=
种取法,所以共有1+2+3+…+50=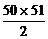 .
.
故取法种数为C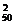 +
+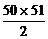 =
=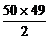 +
+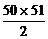 =2500.
=2500.
●思悟小结
7.(理)有11名外语翻译人员,其中5名英语翻译员,4名日语翻译员,另两名英、日语都精通,从中找出8人,使他们组成两个翻译小组,其中4人翻译英文,另4人翻译日文,这两个小组能同时工作,问这样的分配名单共可开出几张?
分析:既精通英语,又精通日语的“多面手”是特殊元素,所以可以从他们的参与情况入手进行分类讨论.
解:按“多面手”的参与情况分成三类.
第一类:多面手不参加,这时有C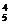 C
C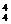 种;
种;
第二类:多面手中有一人入选,这时又有该人参加英文或日文翻译两种可能,因此有C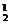 C
C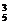 C
C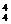 +C
+C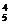 C
C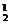 C
C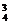 种;
种;
第三类:多面手中两个均入选,这时又分三种情况:两个都译英文、两个都译日文、两人各译一个语种,因此有C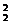 C
C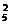 C
C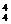 +C
+C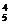 C
C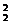 C
C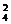 +C
+C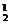 C
C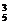 C
C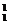 C
C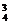 种.
种.
综上分析,共可开出C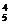 C
C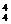 +C
+C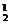 C
C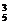 C
C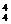 +C
+C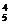 C
C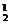 C
C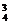 +C
+C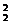 C
C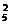 C
C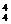 +C
+C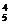 C
C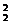 C
C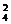 + C
+ C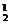 C
C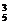 C
C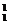 C
C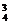 =
=
185种.
评述:首先注意分类方法,体会分类方法在解组合问题中的作用.本题也可以先安排翻译英文人员,后安排翻译日文人员进行分类求解,共有C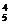 C
C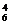 +C
+C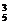 C
C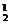 C
C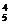 +C
+C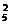 C
C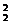 C
C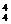 =185种.
=185种.
(文)某市工商局对35种商品进行抽样检查,鉴定结果有15种假货,现从35种商品中选取3种.
(1)其中某一种假货必须在内,不同的取法有多少种?
(2)其中某一种假货不能在内,不同的取法有多少种?
(3)恰有2种假货在内,不同的取法有多少种?
(4)至少有2种假货在内,不同的取法有多少种?
(5)至多有2种假货在内,不同的取法有多少种?
解:(1)C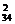 =561.
=561.
(2)C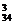 =5984.
=5984.
(3)C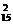 ·C
·C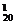 =2100.
=2100.
(4)C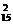 ·C
·C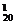 +C
+C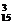 =2555.
=2555.
(5)C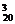 +C
+C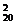 C
C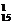 +C
+C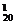 C
C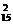 =6090.
=6090.
探究创新
6.袋中有10个球,其中4个红球,6个白球,若取到1个红球记2分,取到1个白球记1分,那么从这10个球中取出4个,使总分不低于5分的取法有多少种?
解法一:取出4个球不低于5分只能是4红或3红1白或2红2白或1红3白.
故有C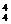 +C
+C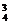 C
C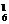 +C
+C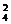 C
C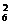 +C
+C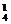 C
C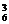 =195种.
=195种.
解法二:取出4个球总分低于5分只能是4个白球,故有C -C
-C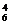 =195种.
=195种.
培养能力
5.某运输公司有7个车队,每个车队的车都多于4辆且型号相同,要从这7个车队中抽出10辆车组成一运输车队,每个队至少抽1辆车,则不同的抽法有多少种?
解:由于每队至少抽1辆,故问题转化为从7个车队中抽3辆车,分类讨论.
①3辆车都从1个队抽,有C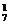 种;②3辆车从2个队抽,有A
种;②3辆车从2个队抽,有A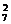 种;③3辆车从3个队抽,有C
种;③3辆车从3个队抽,有C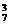 种.
种.
综上所述,共有C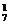 +A
+A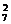 +C
+C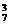 =84种.
=84种.
4.某年级有6个班,派3个数学老师任教,每位教师教两个班,不同的任课方法种数有_______种.
解析:把6个班均匀分为3份,有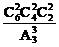 种分法,再把这三份分给3位教师,所以不同的任课方法有
种分法,再把这三份分给3位教师,所以不同的任课方法有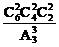 A
A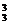 =C
=C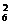 C
C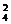 C
C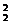 种.
种.
答案:90
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com