
3.(2004年江苏,9)将一颗质地均匀的骰子(它是一种各面上分别标有点数1、2、3、4、5、6的正方体玩具)先后抛掷3次,至少出现一次6点向上的概率是
A. B.
B.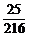 C.
C.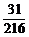 D.
D.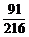
解析:质地均匀的骰子先后抛掷3次,共有6×6×6种结果.3次均不出现6点向上的掷法有5×5×5种结果.由于抛掷的每一种结果都是等可能出现的,所以不出现6点向上的概率为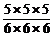 =
=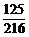 ,由对立事件概率公式,知3次至少出现一次6点向上的概率是1-
,由对立事件概率公式,知3次至少出现一次6点向上的概率是1-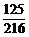 =
= 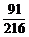 .
.
答案:D
2.(2004年重庆,理11)某校高三年级举行的一次演讲比赛共有10位同学参加,其中一班有3位,二班有2位,其他班有5位.若采取抽签的方式确定他们的演讲顺序,则一班的3位同学恰好被排在一起(指演讲序号相连),而二班的2位同学没有被排在一起的概率为
A.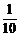 B.
B.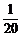 C.
C.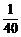 D.
D.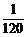
解析:10位同学总参赛次序A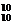 .一班3位同学恰好排在一起,而二班的2位同学没有排在一起的方法数为先将一班3人捆在一起A
.一班3位同学恰好排在一起,而二班的2位同学没有排在一起的方法数为先将一班3人捆在一起A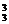 ,与另外5人全排列A
,与另外5人全排列A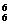 ,二班2位同学不排在一起,采用插空法A
,二班2位同学不排在一起,采用插空法A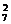 ,即A
,即A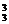 A
A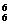 A
A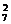 .
.
∴所求概率为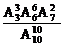 =
= 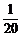 .
.
答案:B
1.(2004年全国Ⅰ,文11)从1,2,…,9这九个数中,随机抽取3个不同的数,则这3个数的和为偶数的概率是
A.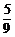 B.
B.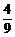 C.
C.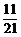 D.
D.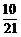
解析:基本事件总数为C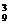 ,设抽取3个数,和为偶数为事件A,则A事件数包括两类:抽取3个数全为偶数,或抽取3数中2个奇数1个偶数,前者C
,设抽取3个数,和为偶数为事件A,则A事件数包括两类:抽取3个数全为偶数,或抽取3数中2个奇数1个偶数,前者C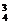 ,后者C
,后者C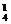 C
C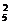 .
.
∴A中基本事件数为C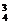 +C
+C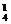 C
C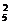 .
.
∴符合要求的概率为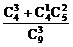 =
= 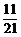 .
.
答案:C
6.使用公式P(A)=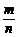 计算时,确定m、n的数值是关键所在,其计算方法灵活多变,没有固定的模式,可充分利用排列组合知识中的分类计数原理和分步计数原理,必须做到不重复不遗漏.
计算时,确定m、n的数值是关键所在,其计算方法灵活多变,没有固定的模式,可充分利用排列组合知识中的分类计数原理和分步计数原理,必须做到不重复不遗漏.
●点击双基
5.等可能性事件的概率:一次试验连同其中可能出现的每一个结果称为一个基本事件,通常此试验中的某一事件A由几个基本事件组成.如果一次试验中可能出现的结果有n个,即此试验由n个基本事件组成,而且所有结果出现的可能性都相等,那么每一基本事件的概率都是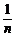 .如果某个事件A包含的结果有m个,那么事件A的概率P(A)=
.如果某个事件A包含的结果有m个,那么事件A的概率P(A)=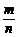 .
.
4.事件A的概率:在大量重复进行同一试验时,事件A发生的频率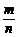 总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A).由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0.
总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A).由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0.
3.不可能事件:在一定条件下不可能发生的事件.
2.必然事件:在一定条件下必然要发生的事件.
1.随机事件:在一定条件下可能发生也可能不发生的事件.
11.1 随机事件的概率
●知识梳理
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com