
2.12 函数的综合问题
●知识梳理
函数的综合应用主要体现在以下几方面:
2.利用判别式法及不等式法求最值时,都需检验等号能否取到.另外,利用判别式法解决问题时,一定要考虑二次项系数可否为零.当二次项系数为零时,不能用判别式法解决问题.
●教师下载中心
教学点睛
利用导数先求极大值和极小值,然后确定最值,也是求函数最值的常用方法.复习本节时应适当渗透导数的有关知识.
拓展题例
[例1] 已知二次函数y=f(x)的最大值等于13,且f(3)=f(-1)=5,求f(x)的解析式.
解:∵f(3)=f(-1),
∴抛物线y=f(x)有对称轴x=1.故可设f(x)=a(x-1)2+13,将点(3,5)代入,求得a=-2.
∴f(x)=-2(x-1)2+13=-2x2+4x+11.
[例2] 已知函数f(x)的定义域为R,且对一切x∈R,都有f(x+2)=f(2-x),f(x+7)=f(7-x).
(1)若f(5)=9,求f(-5)的值;
(2)已知x∈[2,7]时,f(x)=(x-2)2,求当x∈[16,20]时,函数g(x)=2x-f(x)的表达式,并求出g(x)的最大值和最小值.
解:(1)由f(x+2)=f(2-x),f(x+7)=f(7-x)可以发现函数f(x)的图象关于直线x=2,x=7对称,且f(x)=f[(x-2)+2]=f[2-(x-2)]=f(4-x)=f[7-(3+x)]= f[7+(3+x)]=f(10+x).
∴f(x)是以10为周期的周期函数.
∴f(-5)=f(-5+10)=f(5)=9.
(2)根据周期性、图象的对称性,结合图象可得到f(x)=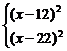
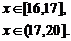
∴g(x)=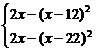
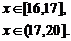
∵x∈[16,17]时,g(x)的最大值为16,最小值为9;x∈(17,20]时,g(x)>g(17)=9,g(x)的最大值为g(20)=36,
∴[g(x)]max=36,[g(x)]min=9.
1.求函数的最值与求函数的值域是同一类问题,都必须熟练掌握本文开头列出的六种方法.
8.已知函数f(x)=x(1-x2),x∈R.
(1)当x>0时,求f(x)的最大值;
(2)当x>0时,指出f(x)的单调性,并用定义证明;
(3)试作出函数f(x)(x∈R)的简图.
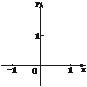
解:(1)∵x>0,欲求f(x)的最大值,必有1-x2>0,
y2=x2(1-x2)2=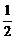 ·2x2(1-x2)(1-x2)≤
·2x2(1-x2)(1-x2)≤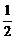 ·[
·[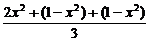 ]3=
]3= ,
,
∴y≤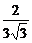 =
=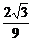 .
.
当且仅当2x2=1-x2,即x=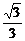 时,取“=”,即f(x)max=f(
时,取“=”,即f(x)max=f(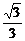 )=
)=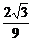 .
.
(2)由(1)知,当x∈(0,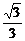 ]时,f(x)单调递增,x∈[
]时,f(x)单调递增,x∈[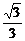 ,+∞)时,f(x)单调递减.
,+∞)时,f(x)单调递减.
设x2>x1>0,则
f(x2)-f(x1)=-x23+x2-(-x13+x1)
=(x2-x1)-(x2-x1)(x22+x1x2+x12)
=(x2-x1)[1-(x22+x1x2+x12)].
当0<x1<x2≤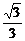 时,x2-x1>0,1-(x22+x1x2+x12)>0.∴f(x2)>f(x1).∴f(x)在(0,
时,x2-x1>0,1-(x22+x1x2+x12)>0.∴f(x2)>f(x1).∴f(x)在(0,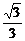 ]上递增.
]上递增.
当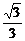 ≤x1<x2时,x2-x1>0,1-(x22+x1x2+x12)<0,∴f(x2)<f(x1).∴f(x)在[
≤x1<x2时,x2-x1>0,1-(x22+x1x2+x12)<0,∴f(x2)<f(x1).∴f(x)在[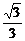 ,+∞)上递减.
,+∞)上递减.
(3)注:图象过点(-1,0)、(0,0)、(1,0),关于原点对称.
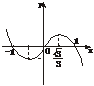
评述:第(1)题也可用导数解决.
∵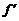 (x)=1-3x2,
(x)=1-3x2,
令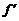 (x)=0,∴x=±
(x)=0,∴x=±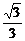 .
.
又x>0,∴x=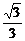 .
.
通过检验单调性知,当x=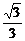 时,f(x)取得最大值,其最大值为
时,f(x)取得最大值,其最大值为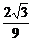 ,以下解法同上.
,以下解法同上.
●思悟小结
7.已知函数g(x)=lg[a(a+1)x2-(3a+1)x+3]的值域是R,求实数a的取值范围.
解:由题意知,应使h(x)=a(a+1)x2-(3a+1)x+3能取到一切正实数.
①a=0时,h(x)=-x+3,显然能取到一切正实数;
②a=-1时,h(x)=2x+3,也能取到一切正实数;
③a≠0且a≠-1时,∵h(x)=a(a+1)x2-(3a+1)x+3是二次函数,
∴必须有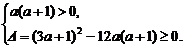
解得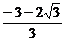 ≤a<-1或0<a≤
≤a<-1或0<a≤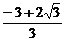 .
.
综上所述,a的取值范围是
[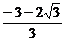 ,-1]∪[0,
,-1]∪[0,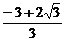 ].
].
探究创新
6.设函数f(x)=x2+x+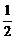 的定义域是[n,n+1](n∈N),问f(x)的值域中有多少个整数?
的定义域是[n,n+1](n∈N),问f(x)的值域中有多少个整数?
解:∵f(x)=(x+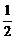 )2+
)2+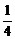 的图象是以(-
的图象是以(-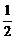 ,
,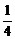 )为顶点,开口向上的抛物线,而自然数n>-
)为顶点,开口向上的抛物线,而自然数n>-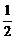 ,∴f(x)的值域是[f(n),f(n+1)],即[n2+n+
,∴f(x)的值域是[f(n),f(n+1)],即[n2+n+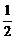 ,n2+3n+
,n2+3n+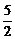 ].其中最小的整数是n2+n+1,最大的整数是n2+3n+2,共有(n2+3n+2)-(n2+n+1)+1=2n+2个整数.
].其中最小的整数是n2+n+1,最大的整数是n2+3n+2,共有(n2+3n+2)-(n2+n+1)+1=2n+2个整数.
5.求函数y=|x|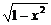 的最值.
的最值.
解:三角代换.设x=cosθ,θ∈[0,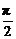 ],
],
(f(x)是偶函数,不必取θ∈[0,π])则y=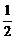 sin2θ.∴ymax=
sin2θ.∴ymax=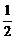 ,ymin=0.
,ymin=0.
培养能力
4.函数y=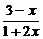 (x≥0)的值域是______________.
(x≥0)的值域是______________.
解析:由y=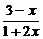 (x≥0),得x=
(x≥0),得x=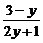 ≥0.
≥0.
∴-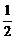 <y≤3.
<y≤3.
答案:(-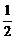 ,3]
,3]
3.(2005年北京海淀模拟题)设函数f(x)的定义域为R,若存在常数M>0,使|f(x)|≤M|x|对一切实数x均成立,则称f(x)为F函数.给出下列函数:
①f(x)=0;②f(x)=x2;③f(x)=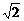 (sinx+cosx);④f(x)=
(sinx+cosx);④f(x)=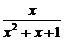 ;⑤f(x)是定义在R上的奇函数,且满足对一切实数x1、x2,均有|f(x1)-f(x2)|≤2|x1-x2|.
;⑤f(x)是定义在R上的奇函数,且满足对一切实数x1、x2,均有|f(x1)-f(x2)|≤2|x1-x2|.
其中是F函数的序号为___________________.
答案:①④⑤
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com