
4.袋中有4只红球3只黑球,从袋中任取4只球,取到1只红球得1分,取到1只黑球得3分,设得分为随机变量ξ,则P(ξ≤6)=________.
解析:取出的4只球中红球个数可能为4,3,2,1个,黑球相应个数为0,1,2,3个.其分值为ξ=4,6,8,10分.P(ξ≤6)=P(ξ=4)+P(ξ=6)=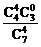 +
+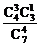 =
=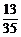 .
.
答案: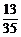
3.现有一大批种子,其中优质良种占30%,从中任取5粒,记ξ为5粒中的优质良种粒数,则ξ的分布列是________.
解析:ξ-B(5,0.3),ξ的分布列是P(ξ=k)=C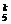 0.3k0.75-k,k=0,1,…,5.
0.3k0.75-k,k=0,1,…,5.
答案:P(ξ=k)=C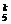 0.3k0.75-k,k=0,1,…,5
0.3k0.75-k,k=0,1,…,5
2.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则P(ξ=12)等于
A.C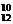 (
(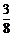 )10·(
)10·(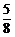 )2 B.C
)2 B.C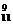 (
(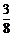 )9(
)9(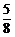 )2·
)2·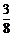
C.C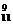 (
(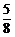 )9·(
)9·(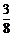 )2 D.C
)2 D.C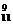 (
(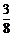 )9·(
)9·(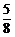 )2
)2
解析:P(ξ=12)表示第12次为红球,前11次中有9次为红球,从而P(ξ=12)=C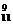 ·(
·(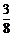 )9(
)9(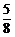 )2×
)2×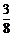 .
.
答案:B
1.袋中有大小相同的5个球,分别标有1,2,3,4,5五个号码,现在在有放回抽取的条件下依次取出两个球,设两个球号码之和为随机变量ξ,则ξ所有可能取值的个数是
A.5 B.9 C.10 D.25
解析:号码之和可能为2,3,4,5,6,7,8,9,10,共9种.
答案:B
2.本题若改为取出后放回,如何求解?
●闯关训练
夯实基础
1.ξ=4时有哪些情况?
5.设随机变量ξ-B(2,p),η-B(4,p),若P(ξ≥1)=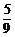 ,则P(η≥1)=______.
,则P(η≥1)=______.
解析:P(ξ≥1)=1-P(ξ<1)=1-C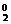 p0·(1-p)2=
p0·(1-p)2=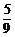 ,
,
∴p=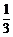 ,P(η≥1)=1-P(η=0)=1-C
,P(η≥1)=1-P(η=0)=1-C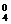 (
(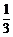 )0(
)0(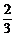 )4=1-
)4=1-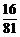 =
=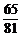 .
.
答案: 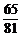
●典例剖析
[例1] 在10件产品中有2件次品,连续抽3次,每次抽1件,求:
(1)不放回抽样时,抽到次品数ξ的分布列;
(2)放回抽样时,抽到次品数η的分布列.
剖析:随机变量ξ可以取0,1,2,η也可以取0,1,2,3,放回抽样和不放回抽样对随机变量的取值和相应的概率都产生了变化,要具体问题具体分析.
解:(1)P(ξ=0)=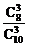 =
=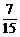 ,P(ξ=1)=
,P(ξ=1)=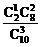 =
=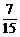 ,
,
P(ξ=2)=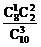 =
= ,
,
所以ξ的分布列为
|
ξ |
0 |
1 |
2 |
|
P |
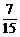 |
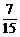 |
 |
(2)P(η=k)=C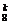 ·0.83-k·0.2k(k=0,1,2,3),所以η的分布列为
·0.83-k·0.2k(k=0,1,2,3),所以η的分布列为
|
η |
0 |
1 |
2 |
3 |
|
P |
C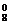 0.83 0.83 |
C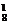 0.82·0.2 0.82·0.2 |
C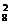 0.8·0.22 0.8·0.22 |
C 0.23 0.23 |
评述:放回抽样时,抽到的次品数为独立重复试验事件,即η-B(3,0.8).
特别提示
求离散型随机变量分布列要注意两个问题:一是求出随机变量所有可能的值;二是求出取每一个值时的概率.
[例2] 一袋中装有5只球,编号为1,2,3,4,5,在袋中同时取3只,以ξ表示取出的三只球中的最小号码,写出随机变量ξ的分布列.
剖析:因为在编号为1,2,3,4,5的球中,同时取3只,所以小号码可能是1或2或3,即ξ可以取1,2,3.
解:随机变量ξ的可能取值为1,2,3.
当ξ=1时,即取出的三只球中最小号码为1,则其他两只球只能在编号为2,3,4,5的四只球中任取两只,故有P(ξ=1)=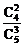 =
=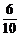 =
=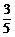 ;
;
当ξ=2时,即取出的三只球中最小号码为2,则其他两只球只能在编号为3,4,5的三只球中任取两只,故有P(ξ=2)=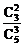 =
=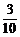 ;
;
当ξ=3时,即取出的三只球中最小号码为3,则其他两只球只能在编号为4,5的两只球中任取两只,故有P(ξ=3)=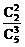 =
=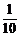 .
.
因此,ξ的分布列如下表所示:
|
ξ |
1 |
2 |
3 |
|
P |
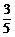 |
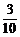 |
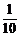 |
评述:求随机变量的分布列,重要的基础是概率的计算,如古典概率、互斥事件的概率、相互独立事件同时发生的概率、n次独立重复试验有k次发生的概率等.本题中基本事件总数,即n=C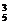 ,取每一个球的概率都属古典概率(等可能性事件的概率).
,取每一个球的概率都属古典概率(等可能性事件的概率).
[例3] (2004年春季安徽)已知盒中有10个灯泡,其中8个正品,2个次品.需要从中取出2个正品,每次取出1个,取出后不放回,直到取出2个正品为止.设ξ为取出的次数,求ξ的分布列及Eξ.
剖析:每次取1件产品,∴至少需2次,即ξ最小为2,有2件次品,当前2次取得的都是次品时,ξ=4,所以ξ可以取2,3,4.
解:P(ξ=2)=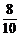 ×
×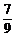 =
=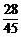 ;
;
P(ξ=3)=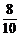 ×
×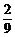 ×
×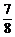 +
+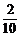 ×
×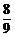 ×
×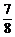 =
=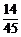 ;
;
P(ξ=4)=1-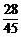 -
-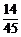 =
= .
.
∴ξ的分布列如下:
|
ξ |
2 |
3 |
4 |
|
P |
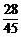 |
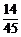 |
 |
Eξ=2×P(ξ=2)+3×P(ξ=3)+4×P(ξ=4)= .
.
评述:本题考查离散型随机变量的分布列和数学期望的概念,考查运用概率知识解决实际问题的能力.
思考讨论
4.某批数量较大的商品的次品率为10%,从中任意地连续取出5件,其中次品数ξ的分布列为________.
解析:本题中商品数量较大,故从中任意抽取5件(不放回)可以看作是独立重复试验n=5,因而次品数ξ服从二项分布,
即ξ-B(5,0.1).
ξ的分布列如下:
|
ξ |
0 |
1 |
2 |
3 |
4 |
5 |
|
P |
0.95 |
0.5×0.94 |
0.1×0.93 |
0.01×0.92 |
4.5×0.14 |
0.15 |
3.已知随机变量ξ的分布列为P(ξ=k)=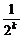 ,k=1,2,…,则P(2<ξ≤4)等于
,k=1,2,…,则P(2<ξ≤4)等于
A.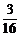 B.
B.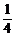 C.
C.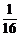 D.
D.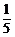
解析:P(2<ξ≤4)=P(ξ=3)+P(ξ=4)=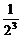 +
+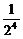 =
=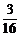 .
.
答案:A
2.下列表中能成为随机变量ξ的分布列的是
A.
|
ξ |
-1 |
0 |
1 |
|
P |
0.3 |
0.4 |
0.4 |
B.
|
ξ |
1 |
2 |
3 |
|
P |
0.4 |
0.7 |
-0.1 |
C.
|
ξ |
-1 |
0 |
1 |
|
P |
0.3 |
0.4 |
0.3 |
D.
|
ξ |
1 |
2 |
3 |
|
P |
0.3 |
0.4 |
0.4 |
解析:A、D不满足分布列的基本性质②,B不满足分布列的基本性质①.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com