2.数学归纳法的应用：①证恒等式；②整除性的证明；③探求平面几何中的问题；④探求数列的通项；⑤不等式的证明.

特别提示

(1)用数学归纳法证题时，两步缺一不可;

(2)证题时要注意两凑：一凑归纳假设；二凑目标.

●点击双基

1.数学归纳法的定义：由归纳法得到的与自然数有关的数学命题常采用下面的证明方法：(1)先证明当n=n₀(n₀是使命题成立的最小自然数)时命题成立；(2)假设当n=k(k∈N*， k≥n₀)时命题成立，再证明当n=k+1时命题也成立，那么就证明这个命题成立，这种证明方法叫数学归纳法.

13.1　 数学归纳法

●知识梳理

1.数学归纳法、极限

要求：(1)理解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题.

(2)了解数列极限和函数极限的概念.

(3)掌握极限的四则运算法则，会求某些数列与函数的极限.

(4)了解函数连续的意义，理解闭区间上连续函数有最大值和最小值的性质.

●复习方略指南

极限的概念和方法是近代数学的核心内容，微积分学的基本概念、基本方法在现代实践中越来越多的被应用，并在现代数学及相关学科的研究中不断得到进一步的发展.本章的主要内容由两部分组成，一是数学归纳法，二是极限.学习极限时要注意数列极限和函数极限的联系和区别、函数的极限与函数连续性的渐进性.

2.总体分布估计的两种情况比较

以上两种情况的不同之处在于前者的频率分布表中列出的是几个不同数值的频率，相应的条形图是用其高度来取各个值的频率的；后者的频率分布表中列出的是在各个不同区间内取值的频率，相应的直方图是用图形面积的大小来表示在各个区间内取值的频率.

●教师下载中心

教学点睛

简单随机抽样，有以下特点：

(1)它要求被抽取样本的总体的个体数有限.这样，就便于对其中各个个体被抽取的概率进行分析.

(2)它是从总体中逐个地进行抽取，这样，就便于在抽样实践中进行操作.

(3)它是一种不放回抽样.由于抽样实践中多采用不放回抽样，使其具有较广泛的实用性，而且由于所抽取的样本中没有被重复抽取的个体，便于进行有关的分析和计算.

(4)它是一种等概率抽样.不仅每次从总体中抽取一个个体时，各个个体被抽取的概率相等，而且在整个抽样过程当中，各个个体被抽取的概率相等，从而保证了这种抽样方法的公平性.

频率分布随着样本容量的增大更加接近总体分布，当样本容量无限增大且分组的组距无限缩小时，频率分布直方图就会演变成一条光滑曲线--反映总体分布的频率密度曲线，基于频率分布与相应的总体分布的关系，且通常我们并不知道一个总体的分布，因此，我们往往是从总体中抽取一个样本，用样本的频率分布去估计相应的总体分布.

统计中假设检验的基本思想是：根据小概率事件在一次试验中几乎不可能发生的原理和从总体中抽测的个体的数值，对事先所作的统计假设作出判断：是拒绝假设，还是接受假设.

拓展例题

[例题] 设有一样本x₁，x₂，…，x_n，其标准差为s_x，另有一样本y₁，y₂，…，y_n，其中y_i=3x_i+2(i=1，2，…，n)，其标准差为s_y，求证：s_y=3s_x.

证明：∵=，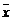

∴=

=

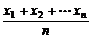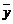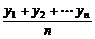
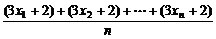
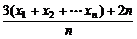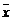==3+2.

∴s_y²=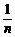［(y₁²+y₂²+…+y_n²)－n 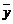²］

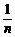=［(3x₁+2)²+(3x₂+2)²+…+(3x_n+2)²－n(3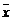+2)²］

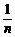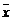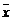=［9(x₁²+x₂²+…+x_n²)+12(x₁+x₂+…+x_n)+4n－n(9²+12+4)］

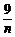=［(x₁²+x₂²+…+x_n²)－n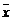²］

=9s_x².

∵s_x≥0，s_y≥0，

∴s_y=3s_x.

1.抽样三种方法比较

8.一个容量为100的样本，数据的分组和各组的一些相关信息如下：

(1)完成上表；

(2)画出频率分布直方图和累积频率分布图；

(3)根据累积频率分布图，总体中小于22的样本数据大约占多大的百分比?

解：(1)

(2)频率分布直方图及累积频率分布图如下：

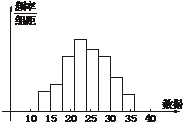
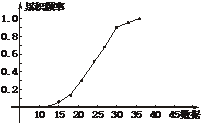
(3)在这个累积频率分布图上，

横坐标为22，

落在21-24的区间内，

折线图在这段区间上的线段所在的直线方程是y－0.3=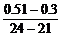(x－21)，

即y=0.07x－1.17.

当x=22时，y=1.54－0.17=0.37.

因此，总体中小于22的数据大约占37%.

●思悟小结

7.一投资者在两个投资方案中选择一个，这两个投资方案的利润x(万元)分别服从正态分布N(8，3²)和N(6，2²)，投资者要求利润超过5万元的概率尽量地大，那么他应选择哪一个方案?

解：对第一个方案，有x-N(8，3²)，于是P(x>5)=1－P(x≤5)=1－F(5)=1－Φ(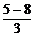)=1－Φ(－1)=1－［1－Φ(1)]=Φ(1)=0.8413.

对第二个方案，有x-N(6，2²)，于是P(x>5)=1－P(x≤5)=1－F(5)=1－Φ(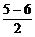)=1－Φ(－0.5)=Φ(0.5)=0.6915.

相比之下，“利润超过5万元”的概率以第一个方案为好，可选第一个方案.

探究创新

6.公共汽车门的高度是按照确保99%以上的成年男子头部不跟车门顶部碰撞设计的，如果某地成年男子的身高ξ-N(173，7²)(cm)，问车门应设计多高？

解：设公共汽车门的设计高度为x cm，由题意，需使P(ξ≥x)＜1%.

∵ξ-N(173，7²)，∴P(ξ≤x)=Φ(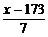)＞0.99.

查表得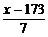＞2.33，∴x＞189.31，即公共汽车门的高度应设计为190 cm，可确保99%以上的成年男子头部不跟车门顶部碰撞.

培养能力

5.随机变量ξ服从正态分布N(0，1)，如果P(ξ<1)=0.8413，求P(－1<ξ<0).

解：∵ξ-N(0，1)，∴P(－1<ξ<0)=P(0<ξ<1)=Φ(1)－Φ(0)=0.8413－0.5=0.3413.