3.(2004年浙江，8)在△ABC中，“A＞30°”是“sinA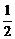＞”的

A.充分而不必要条件　　　　　　　　　　　　　　　　　　　 B.必要而不充分条件

C.充分必要条件　　　　　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

解析：在△ABC中，A＞30°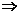0＜sinA＜1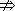sinA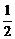＞，sinA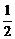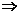＞30°＜A＜150°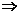

A＞30°.

∴“A＞30°”是“sinA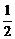＞”的必要不充分条件.

答案：B

2.(2004年湖北，理4)已知a、b、c为非零的平面向量.甲：a·b=a·c，乙：b=c，则

A.甲是乙的充分条件但不是必要条件

B.甲是乙的必要条件但不是充分条件

C.甲是乙的充要条件

D.甲既不是乙的充分条件也不是乙的必要条件

解析：命题甲:a·b=a·c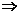a·(b－c)=0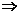a=0或b=c.

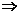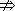命题乙:b=c，因而乙甲，但甲乙.

故甲是乙的必要条件但不是充分条件.

答案：B

1.ac²＞bc²是a＞b成立的

A.充分而不必要条件　　　　　　　　　　　　　　　　　　　 B.充要条件

C.必要而不充分条件　　　　　　　　　　　　　　　　　　　 D.既不充分也不必要条件

解析：a＞b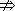ac²＞bc²，如c=0.

答案：A

4.反证法：当直接证明有困难时，常用反证法.

●点击双基

3.充要条件：如果既有p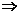q，又有q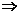p，记作p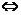q，则p叫做q的充分必要条件，简称充要条件，原命题和逆命题(或逆否命题和否命题)都成立，命题中的条件是充要的.

2.必要条件：如果q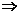p，则p叫q的必要条件，逆命题(或否命题)成立，命题中的条件为必要的，也可称q是p的充分条件.

1.充分条件：如果p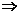q，则p叫q的充分条件，原命题(或逆否命题)成立，命题中的条件是充分的，也可称q是p的必要条件.

1.3　 充要条件与反证法

●知识梳理

2.要明确原命题、否命题、逆命题、逆否命题之间的关系.

拓展题例

[例1] 写出下列各命题的否定及其否命题，并判断它们的真假.

(1)若x、y都是奇数，则x+y是偶数；

(2)若xy=0，则x=0或y=0；

(3)若一个数是质数，则这个数是奇数.

解：(1)命题的否定：x、y都是奇数，则x+y不是偶数，为假命题.

原命题的否命题：若x、y不都是奇数，则x+y不是偶数，是假命题.

(2)命题的否定：xy=0则x≠0且y≠0，为假命题.

原命题的否命题：若xy≠0，则x≠0且y≠0，是真命题.

(3)命题的否定：一个数是质数，则这个数不是奇数，是假命题.

原命题的否命题：若一个数不是质数，则这个数不是奇数，为假命题.

[例2] 有A、B、C三个盒子，其中一个内放有一个苹果，在三个盒子上各有一张纸条.

A盒子上的纸条写的是“苹果在此盒内”，

B盒子上的纸条写的是“苹果不在此盒内”，

C盒子上的纸条写的是“苹果不在A盒内”.

如果三张纸条中只有一张写的是真的，请问苹果究竟在哪个盒子里？

解：若苹果在A盒内，则A、B两个盒子上的纸条写的为真，不合题意.

若苹果在B盒内，则A、B两个盒子上的纸条写的为假，C盒子上的纸条写的为真，符合题意，即苹果在B盒内.

同样，若苹果在C盒内，则B、C两盒子上的纸条写的为真，不合题意.

综上，苹果在B盒内.

2.原命题与它的逆否命题同为真假，原命题的逆命题与否命题同为真假，所以对一些命题的真假判断(或推证)，我们可通过对与它同真假的(具有逆否关系的)命题来判断(或推证).

●教师下载中心

教学点睛