
8.在二项式(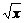 +
+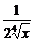 )n的展开式中,前三项的系数成等差数列,求展开式中的有理项.
)n的展开式中,前三项的系数成等差数列,求展开式中的有理项.
分析:根据题意列出前三项系数关系式,先确定n,再分别求出相应的有理项.
解:前三项系数为C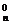 ,
,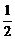 C
C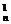 ,
,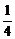 C
C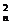 ,由已知C
,由已知C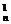 =C
=C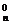 +
+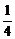 C
C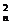 ,即n2-9n+8=0,
,即n2-9n+8=0,
解得n=8或n=1(舍去).
T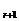 =C
=C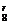 (
(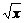 )8-r(2
)8-r(2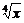 )-r=C
)-r=C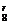 ·
·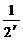 ·x
·x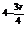 .
.
∵4-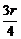 ∈Z且0≤r≤8,r∈Z,
∈Z且0≤r≤8,r∈Z,
∴r=0,r=4,r=8.∴展开式中x的有理项为T1=x4,T5=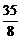 x,T9=
x,T9=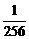 x-2.
x-2.
评述:展开式中有理项的特点是字母x的指数4-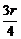 ∈Z即可,而不需要指数4-
∈Z即可,而不需要指数4-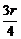 ∈N.
∈N.
探究创新
7.在二项式(axm+bxn)12(a>0,b>0,m、n≠0)中有2m+n=0,如果它的展开式里最大系数项恰是常数项.
(1)求它是第几项;(2)求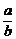 的范围.
的范围.
解:(1)设T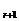 =C
=C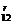 (axm)12-r·(bxn)r=C
(axm)12-r·(bxn)r=C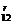 a12-rbrxm(12-r)+nr为常数项,则有m(12-r)+nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
a12-rbrxm(12-r)+nr为常数项,则有m(12-r)+nr=0,即m(12-r)-2mr=0,∴r=4,它是第5项.
(2)∵第5项又是系数最大的项,
|
 C
C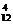 a8b4≥C
a8b4≥C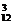 a9b3,
①
a9b3,
①
C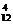 a8b4≥C
a8b4≥C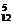 a7b5.
②
a7b5.
②
由①得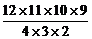 a8b4≥
a8b4≥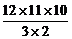 a9b3,
a9b3,
∵a>0,b>0,∴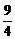 b≥a,即
b≥a,即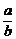 ≤
≤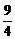 .
.
由②得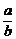 ≥
≥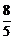 ,∴
,∴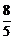 ≤
≤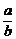 ≤
≤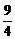 .
.
6.若(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11.
求:(1)a1+a2+a3+…+a11;
(2)a0+a2+a4+…+a10.
解:(1)(1+x)6(1-2x)5=a0+a1x+a2x2+…+a11x11.令x=1,得
a0+a1+a2+…+a11=-26, ①
又a0=1,
所以a1+a2+…+a11=-26-1=-65.
(2)再令x=-1,得
a0-a1+a2-a3+…-a11=0. ②
①+②得a0+a2+…+a10=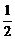 (-26+0)=-32.
(-26+0)=-32.
评述:在解决此类奇数项系数的和、偶数项系数的和的问题中常用赋值法,令其中的字母等于1或-1.
5.已知(x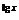 +1)n展开式中,末三项的二项式系数和等于22,二项式系数最大项为20000,求x的值.
+1)n展开式中,末三项的二项式系数和等于22,二项式系数最大项为20000,求x的值.
解:由题意C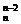 +C
+C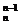 +C
+C =22,
=22,
即C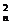 +C
+C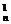 +C
+C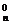 =22,
=22,
∴n=6.∴第4项的二项式系数最大.
∴C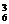 (x
(x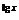 )3=20000,即x3lgx=1000.
)3=20000,即x3lgx=1000.
∴x=10或x=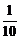 .
.
培养能力
4.(2004年湖南,理15)若(x3+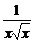 )n的展开式中的常数项为84,则n=_____________.
)n的展开式中的常数项为84,则n=_____________.
解析:T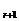 =C
=C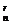 (x3)n-r·(x
(x3)n-r·(x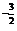 )r=C
)r=C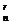 ·x
·x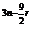 .
.
令3n-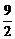 r=0,∴2n=3r.
r=0,∴2n=3r.
∴n必为3的倍数,r为偶数.
试验可知n=9,r=6时,C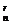 =C
=C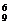 =84.
=84.
答案:9
3.(2004年全国Ⅳ,13)(x-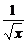 )8展开式中x5的系数为_____________.
)8展开式中x5的系数为_____________.
解析:设展开式的第r+1项为T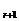 =C
=C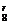 x8-r·(-
x8-r·(-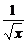 )r=(-1)rC
)r=(-1)rC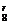 x
x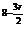 .
.
令8-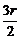 =5得r=2时,x5的系数为(-1)2·C
=5得r=2时,x5的系数为(-1)2·C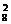 =28.
=28.
答案:28
2.(2004年福建,文9)已知(x-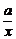 )8展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是
)8展开式中常数项为1120,其中实数a是常数,则展开式中各项系数的和是
A.28 B.38 C.1或38 D.1或28
解析:T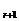 =C
=C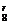 ·x8-r·(-ax-1)r=(-a)rC
·x8-r·(-ax-1)r=(-a)rC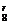 ·x8-2r.
·x8-2r.
令8-2r=0,∴r=4.
∴(-a)4C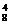 =1120.∴a=±2.
=1120.∴a=±2.
当a=2时,令x=1,则(1-2)8=1.
当a=-2时,令x=-1,则(-1-2)8=38.
答案:C
1.一串装饰彩灯由灯泡串联而成,每串有20个灯泡,只要有一只灯泡坏了,整串灯泡就不亮,则因灯泡损坏致使一串彩灯不亮的可能性的种数为
A.20 B.219 C.220 D.220-1
解析:C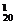 +C
+C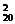 +…+C
+…+C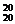 =220-1.
=220-1.
答案:D
5.若(x+1)n=xn+…+ax3+bx2+cx+1(n∈N*),且a∶b=3∶1,那么n=_____________.
解析:a∶b=C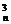 ∶C
∶C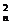 =3∶1,n=11.
=3∶1,n=11.
答案:11
●典例剖析
[例1] 如果在(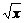 +
+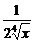 )n的展开式中,前三项系数成等差数列,求展开式中的有理项.
)n的展开式中,前三项系数成等差数列,求展开式中的有理项.
解:展开式中前三项的系数分别为1,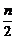 ,
,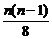 ,
,
由题意得2×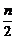 =1+
=1+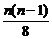 ,得n=8.
,得n=8.
设第r+1项为有理项,T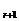 =C
=C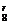 ·
·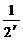 ·x
·x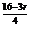 ,则r是4的倍数,所以r=0,4,8.
,则r是4的倍数,所以r=0,4,8.
有理项为T1=x4,T5=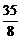 x,T9=
x,T9=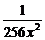 .
.
评述:求展开式中某一特定的项的问题常用通项公式,用待定系数法确定r.
[例2] 求式子(|x|+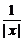 -2)3的展开式中的常数项.
-2)3的展开式中的常数项.
解法一:(|x|+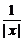 -2)3=(|x|+
-2)3=(|x|+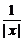 -2)(|x|+
-2)(|x|+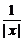 -2)(|x|+
-2)(|x|+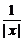 -2)得到常数项的情况有:①三个括号中全取-2,得(-2)3;②一个括号取|x|,一个括号取
-2)得到常数项的情况有:①三个括号中全取-2,得(-2)3;②一个括号取|x|,一个括号取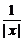 ,一个括号取-2,得C
,一个括号取-2,得C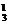 C
C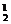 (-2)=-12,
(-2)=-12,
∴常数项为(-2)3+(-12)=-20.
解法二:(|x|+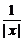 -2)3=(
-2)3=(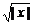 -
-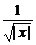 )6.
)6.
设第r+1项为常数项,
则T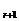 =C
=C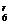 ·(-1)r·(
·(-1)r·(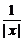 )r·|x|
)r·|x|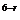 =(-1)6·C
=(-1)6·C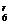 ·|x|
·|x|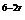 ,得6-2r=0,r=3.
,得6-2r=0,r=3.
∴T3+1=(-1)3·C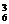 =-20.
=-20.
思考讨论
(1)求(1+x+x2+x3)(1-x)7的展开式中x4的系数;
(2)求(x+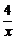 -4)4的展开式中的常数项;
-4)4的展开式中的常数项;
(3)求(1+x)3+(1+x)4+…+(1+x)50的展开式中x3的系数.
解:(1)原式=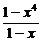 (1-x)7=(1-x4)(1-x)6,展开式中x4的系数为(-1)4C
(1-x)7=(1-x4)(1-x)6,展开式中x4的系数为(-1)4C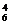 -
-
1=14.
(2)(x+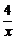 -4)4=
-4)4=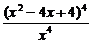 =
=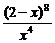 ,展开式中的常数项为C
,展开式中的常数项为C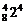 ·(-1)4=1120.
·(-1)4=1120.
(3)方法一:原式=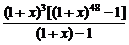 =
=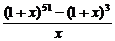 .
.
展开式中x3的系数为C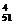 .
.
方法二:原展开式中x3的系数为
C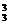 +C
+C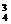 +C
+C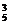 +…+C
+…+C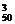 =C
=C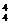 +C
+C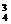 +…+C
+…+C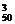 =C
=C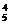 +C
+C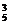 +…+C
+…+C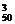 =…=C
=…=C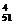 .
.
评述:把所给式子转化为二项展开式形式是解决此类问题的关键.
[例3] 设an=1+q+q2+…+q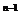 (n∈N*,q≠±1),An=C
(n∈N*,q≠±1),An=C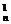 a1+C
a1+C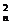 a2+…+C
a2+…+C an.
an.
(1)用q和n表示An;
(2)(理)当-3<q<1时,求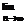
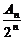 .
.
解:(1)因为q≠1,
所以an=1+q+q2+…+q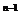 =
=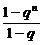 .
.
于是An=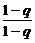 C
C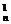 +
+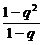 C
C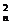 +…+
+…+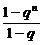 C
C
=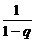 [(C
[(C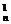 +C
+C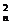 +…+C
+…+C )-(C
)-(C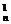 q+C
q+C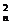 q2+…+C
q2+…+C qn)]
qn)]
=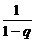 {(2n-1)-[(1+q)n-1]}
{(2n-1)-[(1+q)n-1]}
=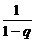 [2n-(1+q)n].
[2n-(1+q)n].
(2)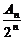 =
=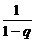 [1-(
[1-(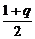 )n].
)n].
因为-3<q<1,且q≠-1,
所以0<|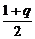 |<1.
|<1.
所以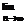
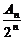 =
=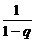 .
.
●闯关训练
夯实基础
4.(2004年湖北,文14)已知(x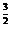 +x
+x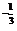 )n的展开式中各项系数的和是128,则展开式中x5的系数是_____________.(以数字作答)
)n的展开式中各项系数的和是128,则展开式中x5的系数是_____________.(以数字作答)
解析:∵(x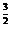 +x
+x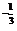 )n的展开式中各项系数和为128,
)n的展开式中各项系数和为128,
∴令x=1,即得所有项系数和为2n=128.
∴n=7.设该二项展开式中的r+1项为T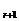 =C
=C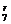 (x
(x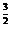 )
)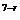 ·(x
·(x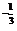 )r=C
)r=C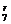 ·x
·x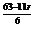 ,
,
令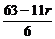 =5即r=3时,x5项的系数为C
=5即r=3时,x5项的系数为C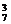 =35.
=35.
答案:35
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com