
3.会用导数研究多项式函数的单调性,会求多项式函数的单调区间.
2.理解导数的物理、几何意义,会求函数在某点处切线的斜率和物体运动到某点处的瞬时速度.
1.理解导数的定义,会求多项式函数的导数.
2.数学归纳法在考试中时隐时现,且较隐蔽,因此在复习中应引起重视.只要与自然数有关,都可考虑数学归纳法,当然主要是恒等式、等式、不等式、整除问题、几何问题、三角问题、数列问题等联系得更多一些.
拓展题例
[例1] 是否存在正整数m,使得f(n)=(2n+7)·3n+9对任意自然数n都能被m整除?若存在,求出最大的m值,并证明你的结论;若不存在,请说明理由.
解:由f(n)=(2n+7)·3n+9,得f(1)=36, f(2)=3×36, f(3)=10×36, f(4)=
34×36,由此猜想m=36.
下面用数学归纳法证明:
(1)当n=1时,显然成立.
(2)假设n=k时, f(k)能被36整除,即f(k)=(2k+7)·3k+9能被36整除;当n=k+1时,[2(k+1)+7]·3k+1+9=3[(2k+7)·3k+9]+18(3k-1-1),
由于3k-1-1是2的倍数,故18(3k-1-1)能被36整除.这就是说,当n=k+1时,f(n)也能被36整除.
由(1)(2)可知对一切正整数n都有f(n)=(2n+7)·3n+9能被36整除,m的最大值为36.
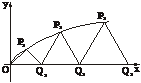
[例2] 如下图,设P1,P2,P3,…,Pn,…是曲线y=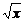 上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=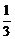 n(n+1).
n(n+1).
证明:(1)当n=1时,点P1是直线y=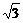 x与曲线y=
x与曲线y=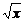 的交点,
的交点,
∴可求出P1(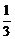 ,
,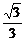 ).
).
∴a1=|OP1|=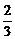 .而
.而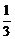 ×1×2=
×1×2=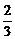 ,命题成立.
,命题成立.
(2)假设n=k(k∈N*)时命题成立,即a1+a2+…+ak=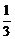 k(k+1),则点Qk的坐标为(
k(k+1),则点Qk的坐标为(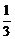 k(k+1),0),
k(k+1),0),
∴直线QkPk+1的方程为y=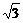 [x-
[x-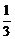 k(k+1)].代入y=
k(k+1)].代入y=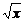 ,解得Pk+1点的坐标为
,解得Pk+1点的坐标为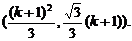
∴ak+1=|QkPk+1|=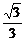 (k+1)·
(k+1)·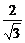 =
=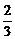 (k+1).
(k+1).
∴a1+a2+…+ak+a k+1=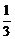 k(k+1)+
k(k+1)+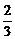 (k+1)=
(k+1)=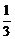 (k+1)(k+2).
(k+1)(k+2).
∴当n=k+1时,命题成立.
由(1)(2)可知,命题对所有正整数都成立.
评述:本题的关键是求出Pk+1的纵坐标,再根据正三角形高与边的关系求出|QkP k+1|.
1.数学归纳法中的归纳思想是比较常见的数学思想,因此要重视.
2.归纳、猜想、论证是培养学生观察能力、归纳能力以及推理论证能力的方式之一.
●教师下载中心
教学点睛
1.用数学归纳法证明问题应注意:
(1)第一步验证n=n0时,n0并不一定是1.
(2)第二步证明的关键是要运用归纳假设,特别要弄清由k到k+1时命题的变化.
(3)由假设n=k时命题成立,证n=k+1时命题也成立,要充分利用归纳假设,要恰当地“凑”出目标.
8.(2004年重庆,22)设数列{an}满足a1=2,an+1=an+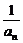 (n=1,2,…).
(n=1,2,…).
(1)证明an>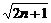 对一切正整数n都成立;
对一切正整数n都成立;
(2)令bn=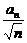 (n=1,2,…),判定bn与bn+1的大小,并说明理由.
(n=1,2,…),判定bn与bn+1的大小,并说明理由.
(1)证法一:当n=1时,a1=2>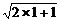 ,不等式成立.
,不等式成立.
假设n=k时,ak>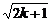 成立,
成立,
当n=k+1时,ak+12=ak2+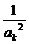 +2>2k+3+
+2>2k+3+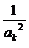 >2(k+1)+1,
>2(k+1)+1,
∴当n=k+1时,ak+1>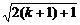 成立.
成立.
综上,由数学归纳法可知,an>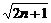 对一切正整数成立.
对一切正整数成立.
证法二:当n=1时,a1=2>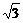 =
=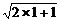 结论成立.
结论成立.
假设n=k时结论成立,即ak>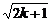 ,
,
当n=k+1时,由函数f(x)=x+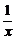 (x>1)的单调递增性和归纳假设有
(x>1)的单调递增性和归纳假设有
ak+1=ak+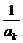 >
>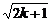 +
+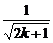 =
=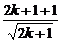 =
=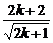 =
=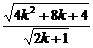 >
>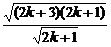 =
=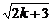 .
.
∴当n=k+1时,结论成立.
因此,an>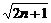 对一切正整数n均成立.
对一切正整数n均成立.
(2)解: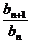 =
=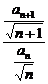 =(1+
=(1+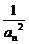 )
)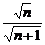 <(1+
<(1+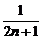 )
)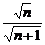 =
=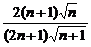 =
= =
=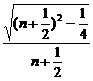 <1.
<1.
故bn+1<bn.
●思悟小结
7.平面内有n条直线,其中无任何两条平行,也无任何三条共点,求证:这n条直线把平面分割成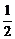 (n2+n+2)块.
(n2+n+2)块.
证明:(1)当n=1时,1条直线把平面分成2块,又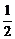 (12+1+2)=2,命题成立.
(12+1+2)=2,命题成立.
(2)假设n=k时,k≥1命题成立,即k条满足题设的直线把平面分成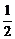 (k2+k+2)块,那么当n=k+1时,第k+1条直线被k条直线分成k+1段,每段把它们所在的平面块又分成了2块,因此,增加了k+1个平面块.所以k+1条直线把平面分成了
(k2+k+2)块,那么当n=k+1时,第k+1条直线被k条直线分成k+1段,每段把它们所在的平面块又分成了2块,因此,增加了k+1个平面块.所以k+1条直线把平面分成了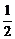 (k2+k+2)+k+1=
(k2+k+2)+k+1= 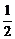 [(k+1)
2+(k+1)+2]块,这说明当n=k+1时,命题也成立.由(1)(2)知,对一切n∈N*,命题都成立.
[(k+1)
2+(k+1)+2]块,这说明当n=k+1时,命题也成立.由(1)(2)知,对一切n∈N*,命题都成立.
探究创新
6.已知数列{bn}是等差数列,b1=1,b1+b2+…+b10=100.
(1)求数列{bn}的通项公式bn;
(2)设数列{an}的通项an=lg(1+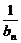 ),记Sn为{an}的前n项和,试比较Sn与
),记Sn为{an}的前n项和,试比较Sn与
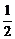 lgbn+1的大小,并证明你的结论.
lgbn+1的大小,并证明你的结论.
解:(1)容易得bn=2n-1.
(2)由bn=2n-1,
知Sn=lg(1+1)+1g(1+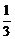 )+…+lg(1+
)+…+lg(1+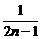 )=lg(1+1)(1+
)=lg(1+1)(1+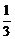 )·…·(1+
)·…·(1+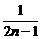 ).
).
又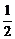 1gbn+1=1g
1gbn+1=1g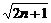 ,
,
因此要比较Sn与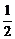 1gbn+1的大小,可先比较(1+1)(1+
1gbn+1的大小,可先比较(1+1)(1+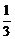 )·…·(1+
)·…·(1+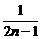 )与
)与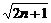 的大小.
的大小.
取n=1,2,3可以发现:前者大于后者,由此推测
(1+1)(1+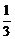 )· …· (1+
)· …· (1+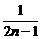 )>
)>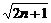 .
①
.
①
下面用数学归纳法证明上面猜想:
当n=1时,不等式①成立.
假设n=k时,不等式①成立,即
(1+1)(1+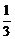 )·…·(1+
)·…·(1+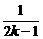 )>
)>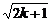 .
.
那么n=k+1时,
(1+1)(1+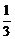 )·…·(1+
)·…·(1+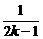 )(1+
)(1+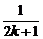 )>
)>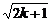 (1+
(1+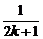 )
)
=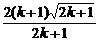 .
.
又[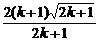 ]2-(
]2-(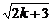 )2=
)2=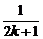 >0,
>0,
∴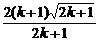 >
>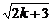 =
=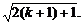
∴当n=k+1时①成立.
综上所述,n∈N*时①成立.
由函数单调性可判定Sn>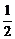 1gbn+1.
1gbn+1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com