
5.5 向量的应用
●知识梳理
理解向量的几何、代数、三角及物理方面的应用,能将当前的问题转化为可用向量解决的问题,培养学生的创新精神和应用能力.
特别提示
许多代数、几何中的问题都可以转化为向量来处理.它不仅能解决数学学科本身的问题,跨学科应用也是它的一个特点.
●点击双基
2.要加大以三角形为背景,以三角恒等变换公式、向量等为工具的小型综合题的训练.
拓展题例
[例1] 已知A、B、C是△ABC的三个内角,y=cotA+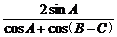 .
.
(1)若任意交换两个角的位置,y的值是否变化?试证明你的结论.(2)求y的最小值.
解:(1)∵y=cotA+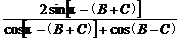
=cot A+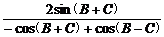
=cot A+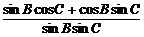
=cotA+cotB+cotC,
∴任意交换两个角的位置,y的值不变化.
(2)∵cos(B-C)≤1,
∴y≥cotA+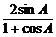 =
=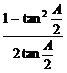 +2tan
+2tan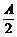 =
=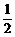 (cot
(cot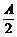 +3tan
+3tan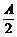 )≥
)≥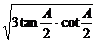 =
=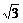 .
.
故当A=B=C=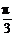 时,ymin=
时,ymin=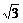 .
.
评述:本题的第(1)问是一道结论开放型题,y的表达式的表面不对称性显示了问题的有趣之处.第(2)问实际上是一道常见题:在△ABC中,求证:cotA+cotB+cotC≥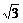 .
.
[例2] 在△ABC中,sinA=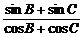 ,判断这个三角形的形状.
,判断这个三角形的形状.
分析:判断一个三角形的形状,可由三个内角的关系确定,亦可由三边的关系确定.采用后一种方法解答本题,就必须“化角为边”.
解:应用正弦定理、余弦定理,可得
a=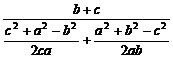 ,所以b(a2-b2)+c(a2-c2)=bc(b+c).所以(b+c)a2=(b3+c3)+bc(b+c).所以a2=b2-bc+c2+bc.所以a2=b2+c2.所以△ABC是直角三角形.
,所以b(a2-b2)+c(a2-c2)=bc(b+c).所以(b+c)a2=(b3+c3)+bc(b+c).所以a2=b2-bc+c2+bc.所以a2=b2+c2.所以△ABC是直角三角形.
评述:恒等变形是学好数学的基本功,变形的方向是关键.若考虑三内角的关系,本题可以从已知条件推出cosA=0.
1.一方面要让学生体会向量方法在解三角形方面的应用,另一方面要让学生体会解三角形是重要的测量手段,通过数值计算进一步提高使用计算器的技能技巧和解决实际问题的能力.
6.用向量的数量积求三角形内角时,需明确向量的夹角与三角形内角是相等还是互补.
●教师下载中心
教学点睛
5.用正(余)弦定理解三角形问题可适当应用向量的数量积求三角形内角与应用向量的模求三角形的边长.
4.根据所给条件确定三角形的形状,主要有两种途径:①化边为角;②化角为边.并常用正弦(余弦)定理实施边角转化.
3.在非直角三角形中,tanA+tanB+tanC=tanA·tanB·tanC.
2.∠A、∠B、∠C成等差数列的充分必要条件是∠B=60°.
1.在△ABC中,∵A+B+C=π,∴sin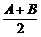 =cos
=cos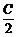 ,cos
,cos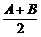 =sin
=sin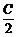 ,tan
,tan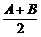 =cot
=cot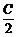 .
.
9.某城市有一条公路,自西向东经过A点到市中心O点后转向东北方向OB,现要修建一条铁路L,L在OA上设一站A,在OB上设一站B,铁路在AB部分为直线段,现要求市中心O与AB的距离为10 km,问把A、B分别设在公路上离中心O多远处才能使|AB|最短?并求其最短距离.(不要求作近似计算)
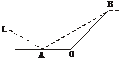
解:在△AOB中,设OA=a,OB=b.
因为AO为正西方向,OB为东北方向,所以∠AOB=135°.
则|AB|2=a2+b2-2abcos135°=a2+b2+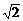 ab≥2ab+
ab≥2ab+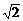 ab=(2+
ab=(2+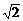 )ab,当且仅当a=b时,“=”成立.又O到AB的距离为10,设∠OAB=α,则∠OBA=45°-α.所以a=
)ab,当且仅当a=b时,“=”成立.又O到AB的距离为10,设∠OAB=α,则∠OBA=45°-α.所以a=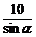 ,b=
,b=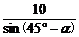 ,
,
ab=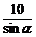 ·
·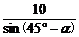
=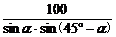
=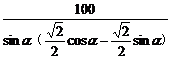
=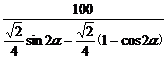
=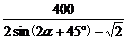 ≥
≥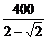 ,
,
当且仅当α=22°30′时,“=”成立.
所以|AB|2≥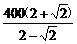 =400(
=400(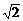 +1)2,
+1)2,
当且仅当a=b,α=22°30′时,“=”成立.
所以当a=b=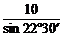 =10
=10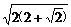 时,|AB|最短,其最短距离为20(
时,|AB|最短,其最短距离为20(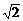 +1),即当AB分别在OA、OB上离O点10
+1),即当AB分别在OA、OB上离O点10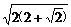 km处,能使|AB|最短,最短距离为20(
km处,能使|AB|最短,最短距离为20(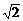 -1).
-1).
●思悟小结
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com