
5.不等式ax2+bx+c>0的解集为{x|2<x<3},则不等式ax2-bx+c>0的解集为_______.
解析:令f(x)=ax2+bx+c,其图象如下图所示,
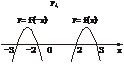
再画出f(-x)的图象即可.
答案:{x|-3<x<-2}
●典例剖析
[例1] 解不等式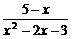 <-1.
<-1.
剖析:这是一个分式不等式,其左边是两个关于x的多项式的商,而右边是非零常数,故需移项通分,右边变为零,再利用商的符号法则,等价转化成整式不等式组.
解:原不等式变为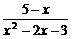 +1<0,
+1<0,
即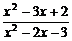 <0
<0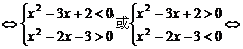 -1<x<1或2<x<3.
-1<x<1或2<x<3.
∴原不等式的解集是{x|-1<x<1或2<x<3}.
[例2] 求实数m的范围,使y=lg[mx2+2(m+1)x+9m+4]对任意x∈R恒有意义.
剖析:mx2+2(m+1)x+9m+4>0恒成立的含义是该不等式的解集为R.
故应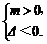
解:由题意知mx2+2(m+1)x+9m+4>0的解集为R,则
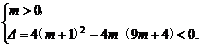
解得m>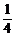 .
.
评述:二次不等式ax2+bx+c>0恒成立的条件: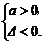
若未说明是二次不等式还应讨论a=0的情况.
思考讨论
本题若要使值域为全体实数,m的范围是什么?
提示:对m分类讨论,m=0适合.
当m≠0时,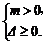 解m即可.
解m即可.
[例3] 若不等式2x-1>m(x2-1)对满足|m|≤2的所有m都成立,求x的取值范围.
剖析:对于m∈[-2,2],不等式2x-1>m(x2-1)恒成立,把m视为主元,利用函数的观点来解决.
解:原不等式化为(x2-1)m-(2x-1)<0.
令f(m)=(x2-1)m-(2x-1)(-2≤m≤2).
则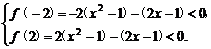
解得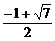 <x<
<x<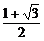 .
.
深化拓展
4.(理)(2003年山东潍坊市第二次模拟考试题)不等式x2-|x-1|-1≤0的解集为____________.
解析:当x-1≥0时,原不等式化为x2-x≤0,解得0≤x≤1.
∴x=1;
当x-1<0时,原不等式化为x2+x-2≤0,
解得-2≤x≤1.∴-2≤x<1.
综上,x≥-2.
答案:{x|-2≤x≤1}
(文)不等式ax2+(ab+1)x+b>0的解集为{x|1<x<2},则a+b=_______.
解析:∵ax2+(ab+1)x+b>0的解集为{x|1<x<2},
∴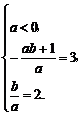 解得
解得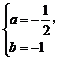 或
或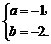
∴a+b=-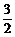 或-3.
或-3.
答案:-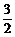 或-3
或-3
3.(2003年重庆市诊断性考试题)已知函数f(x)是R上的增函数,A(0,-1)、B(3,1)是其图象上的两点,那么| f(x+1)|<1的解集是
A.(1,4)
B.(-1,2)
C.(-∞,1]∪[4,+∞)
D.(-∞,-1]∪[2,+∞)
解析:由题意知f(0)=-1,f(3)=1.
又| f(x+1)|<1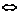 -1<f(x+1)<1,
-1<f(x+1)<1,
即f(0)<f(x+1)<f(3).
又f(x)为R上的增函数,
∴0<x+1<3.∴-1<x<2.
答案:B
2.(2003年北京)若不等式|ax+2|<6的解集为(-1,2),则实数a等于
A.8 B.2 C.-4 D.-8
解析:由|ax+2|<6得-6<ax+2<6,
即-8<ax<4.∵不等式|ax+2|<6的解集为(-1,2),易检验a=-4.
答案:C
1.(2004年全国Ⅳ,5)不等式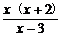 <0的解集为
<0的解集为
A.{x|x<-2或0<x<3}
B.{x|-2<x<0或x>3}
C.{x|x<-2或x>0}
D.{x|x<0或x>3}
解析:在数轴上标出各根.
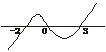
答案:A
3.简单的高次不等式、分式不等式的求解问题可采用“数轴标根法”.
思考讨论
用“数轴标根法”解高次、分式不等式时,对于偶次重根应怎样处理?
●点击双基
2.一元二次不等式的解法.
任何一个一元二次不等式经过不等式的同解变形后,都可以化为ax2+bx+c>0(或<0)(其中a>0)的形式,再根据“大于取两边,小于夹中间”求解集.
1.一元一次不等式的解法.
任何一个一元一次不等式经过不等式的同解变形后,都可以化为ax>b(a≠0)的形式.
当a>0时,解集为{x|x>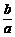 };当a<0时,解集为{x|x<
};当a<0时,解集为{x|x<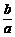 }.
}.
6.4 不等式的解法(一)
●知识梳理
2.本题当|a+b|=0时,不等式成立;
当|a+b|≠0时,原不等式即为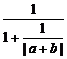 ≤
≤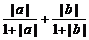 .
.
再利用|a+b|≤|a|+|b|放缩能证吗?读者可以尝试一下!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com