
培养能力
7.求证: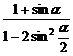 =
=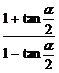 .
.
证明:左边=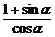 =
=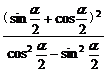 =
=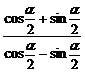 ,
,
右边=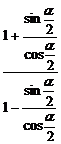 =
=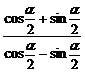 ,
,
∵左边=右边,∴原式成立.
3.角的变换体现出将未知转化为已知的思想方法,这是解决三角中关于角的变换问题常用的数学方法之一.
拓展题例
[例1] 若sinαcosβ=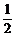 ,求cosαsinβ的取值范围.
,求cosαsinβ的取值范围.
解:令t=cosαsinβ,则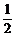 t=
t=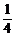 sin2αsin2β.
sin2αsin2β.
∴t=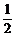 sin2αsin2β∈[-
sin2αsin2β∈[-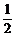 ,
,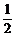 ].
].
[例2] (2004年东北三校高三第一次联考题)已知a=(cos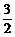 x,sin
x,sin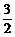 x),b=(cos
x),b=(cos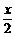 ,-sin
,-sin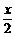 ),x∈[0,
),x∈[0, ].
].
(1)求a·b及|a+b|;
(2)若f(x)=a·b-2λ|a+b|的最小值是-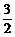 ,求λ的值.
,求λ的值.
解:(1)a·b=cos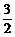 xcos
xcos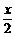 -sin
-sin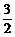 xsin
xsin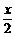 =cos2x.
=cos2x.
|a+b|=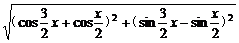 =2
=2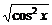 =2cosx(∵x∈[0,
=2cosx(∵x∈[0, ]).
]).
(2)f(x)=cos2x-4λcosx=2(cosx-λ)2-1-2λ2.
∵x∈[0, ],∴cosx∈[0,1].
],∴cosx∈[0,1].
①当λ<0,cosx=0时,f(x)min=-1,矛盾.
②当0≤λ≤1,cosx=λ时,f(x)min=-1-2λ2,由-1-2λ2=-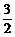 ,得λ=
,得λ=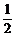 .
.
③当λ>1,cosx=1时,f(x)min=1-4λ,
由1-4λ=-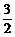 ,得λ=
,得λ=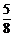 <1,矛盾.
<1,矛盾.
综上,λ=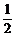 为所求.
为所求.
2.要重视对遇到的问题中角、函数名及其整体结构的分析,提高公式选择的恰当性,有利于缩短运算程序,提高学习效率.
1.公式的熟与准,要依靠理解内涵,明确联系应用,练习尝试,不可机械记忆.
2.常用方法:
(1)直接应用公式.
(2)切割化弦,异名化同名,异角化同角.
(3)形如cosαcos2αcos22α…cos2nα的函数式,只需将分子、分母分别乘以2n+1sinα,应用二倍角正弦公式即可.
●教师下载中心
教学点睛
1.化简要求:
(1)能求出值的应求出值.
(2)使三角函数种数尽量少.
(3)使项数尽量少.
(4)尽量使分母不含三角函数.
(5)尽量使被开方数不含三角函数.
9.将一块圆心角为120°,半径为20 cm的扇形铁片截成一块矩形,如图,有2种裁法:让矩形一边在扇形的一半径OA上或让矩形一边与弦AB平行,请问哪种裁法能得到最大面积的矩形,并求出这个最大值.
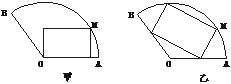
解:对图甲,设∠MOA=θ,则S1=200sin2θ.
∴当θ=45°时,(S1)max=200 cm2.
对图乙,设∠MOA=α,
则S2=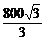 [cos(2α-60°)-cos60°].
[cos(2α-60°)-cos60°].
当α=30°时,(S2)max=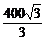 cm2.
cm2.
∵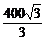 >200,∴用乙种方法好.
>200,∴用乙种方法好.
●思悟小结
8.(2004年湖北,17)已知6sin2α+sinαcosα-2cos2α=0,α∈[ ,π),求
,π),求
sin(2α+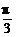 )的值.
)的值.
分析:本题考查三角函数的基本公式以及三角函数式的恒等变形等基础知识和基本运算技能.
解法一:由已知得(3sinα+2cosα)(2sinα-cosα)=0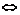 3sinα+2cosα=0或2sinα-cosα=0.
3sinα+2cosα=0或2sinα-cosα=0.
由已知条件可知cosα≠0,所以α≠ ,即α∈(
,即α∈( ,π).
,π).
于是tanα<0,∴tanα=-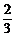 .
.
sin(2α+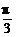 )=sin2αcos
)=sin2αcos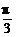 +cos2αsin
+cos2αsin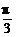
=sinαcosα+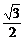 (cos2α-sin2α)
(cos2α-sin2α)
=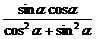 +
+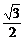 ×
×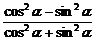 =
=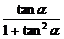 +
+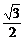 ×
×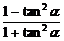 .
.
将tanα=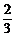 代入上式得
代入上式得
sin(2α+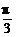 )=
)=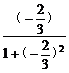 +
+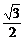 ×
×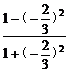 =-
=-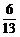 +
+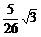 ,即为所求.
,即为所求.
解法二:由已知条件可知cosα≠0,则α≠ ,
,
∴原式可化为6tan2α+tanα-2=0,
即(3tanα+2)(2tanα-1)=0.
又∵α∈( ,π).∴tanα<0,∴tanα=-
,π).∴tanα<0,∴tanα=-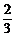 .
.
下同解法一.
探究创新
7.已知f(x)=2asin2x-2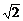 asinx+a+b的定义域是[0,
asinx+a+b的定义域是[0, ],值域是[-5,1],求a、b的值.
],值域是[-5,1],求a、b的值.
解:令sinx=t,∵x∈[0, ],∴t∈[0,1],
],∴t∈[0,1],
f(x)=g(t)=2at2-2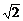 at+a+b
at+a+b
=2a(t-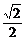 )2+b.
)2+b.
当a>0时,则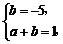
解之得a=6,b=-5.
当a<0时,则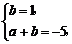
解之得a=-6,b=1.
6.(2004年江苏,17)已知0<α< ,tan
,tan +cot
+cot =
=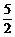 ,求sin(α-
,求sin(α-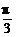 )的值.
)的值.
解:由已知tan +cot
+cot =
=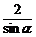 =
=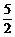 ,得sinα=
,得sinα=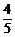 .
.
∵0<α< ,∴cosα=
,∴cosα=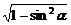 =
=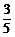 .
.
从而sin(α-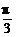 )=sinα·cos
)=sinα·cos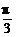 -cosα·sin
-cosα·sin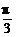
=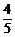 ×
×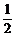 -
-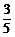 ×
×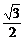 =
=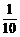 (4-3
(4-3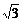 ).
).
培养能力
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com