
2.复习时要构建良好的知识结构.
1.本课复习的重点是:理解向量的基本概念,掌握向量的加法、减法运算,掌握实数与向量的积的运算.
5.培养学生的观察、分析、归纳、抽象的思维能力.
●教师下载中心
教学点睛
4.向量的坐标表示体现了数形的紧密关系,从而可用“数”来证明“形”的问题.
3.对于两个向量平行的充要条件:
a∥b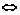 a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.
a=λb,只有b≠0才是正确的.而当b=0时,a∥b是a=λb的必要不充分条件.
2.共线向量和平面向量的两条基本定理,揭示了共线向量和平面向量的基本结构,它们是进一步研究向量的基础.
1.我们学习的向量具有大小和方向两个要素.用有向线段表示向量时,与有向线段起点的位置没有关系.同向且等长的有向线段都表示同一向量.
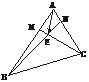
9.在△ABC中,AM∶AB=1∶3,AN∶AC=1∶4,BN与CM交于点E,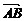 =a,
=a,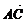 =b,用a、b表示
=b,用a、b表示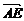 .
.
解:由已知得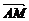 =
=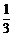
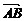 ,
,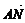 =
=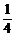
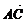 .
.
设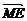 =λ
=λ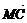 ,λ∈R,则
,λ∈R,则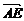 =
=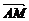 +
+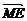 =
=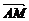 +λ
+λ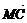 .
.
而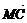 =
=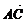 -
-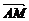 ,
,
∴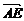 =
=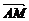 +λ(
+λ(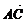 -
-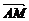 )
)
=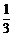
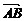 +λ(
+λ(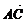 -
-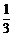
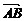 ).
).
∴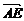 =(
=(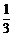 -
-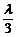 )
)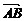 +λ
+λ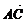 .
.
同理,设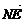 =t
=t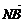 ,t∈R,则
,t∈R,则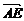 =
=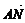 +
+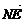 =
=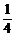
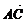 +t
+t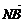 =
=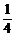
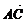 +t(
+t(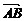 -
-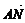 )=
)=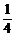
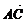 +t(
+t(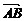 -
-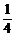
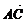 ).
).
∴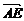 =(
=(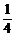 -
-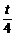 )
)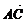 +t
+t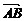 .
.
∴(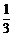 -
-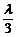 )
)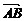 +λ
+λ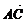 =(
=(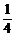 -
-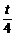 )
)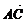 +t
+t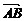 .
.
由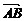 与
与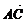 是不共线向量,得
是不共线向量,得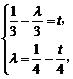
解得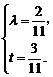 ∴
∴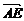 =
=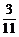
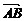 +
+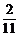
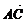 ,
,
即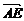 =
=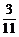 a+
a+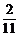 b.
b.
评述:此题所涉及的量较多,且向量与向量之间的关系较为复杂,因此对学生来说确有一定困难.通过共线向量,增加辅助量来理清向量之间关系是“探索”之所在,即对基本定理的深化及应用.
●思悟小结
8.如图所示,D、E是△ABC中AB、AC边的中点,M、N分别是DE、BC的中点,已知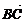 =a,
=a,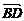 =b,试用a、b分别表示
=b,试用a、b分别表示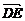 、
、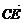 和
和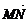 .
.
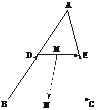
解:由三角形中位线定理,知DE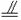
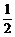 BC.
BC.
故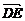 =
=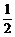
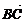 ,即
,即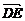 =
=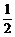 a.
a.
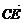 =
=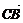 +
+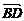 +
+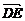 =-a+b+
=-a+b+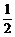 a=-
a=-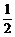 a+b,
a+b,
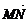 =
=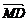 +
+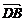 +
+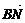 =
=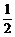
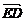 +
+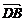 +
+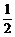
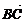 =-
=-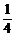 a+
a+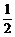 a-b=
a-b=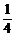 a-b.
a-b.
探究创新
7.已知向量a=2e1-3e2,b=2e1+3e2,其中e1、e2不共线,向量c=2e1-9e2.问是否存在这样的实数λ、μ,使向量d=λa+μb与c共线?
解:∵d=λ(2e1-3e2)+μ(2e1+3e2)
=(2λ+2μ)e1+(-3λ+3μ)e2,
要使d与c共线,则应有实数k,使d=kc,
即(2λ+2μ)e1+(-3λ+3μ)e2=2ke1-9ke2,由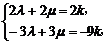 得λ=-2μ.
得λ=-2μ.
故存在这样的实数λ、μ,只要λ=-2μ,就能使d与c共线.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com