
题目列表(包括答案和解析)
2.曲线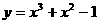 在点P(-1,-1)处的切线方程为 ( )
在点P(-1,-1)处的切线方程为 ( )
A.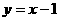 B.
B.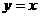 C.
C.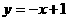 D.
D.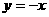
1.直线 、
、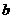 、c两两平行,但不共面,则它们可以确实的平面个数是 ( )
、c两两平行,但不共面,则它们可以确实的平面个数是 ( )
A.1个 B.2个 C.3个 D.6个
21.解 ⑴由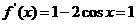 得
得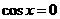 ,
,
当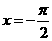 时,
时,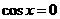 ,此时
,此时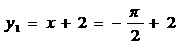 ,
,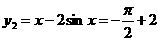 ,
,
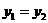 ,所以
,所以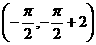 是直线
是直线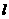 与曲线
与曲线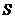 的一个切点;
的一个切点;
当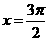 时,
时,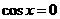 ,此时
,此时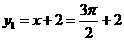 ,
,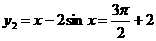 ,
,
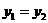 ,所以
,所以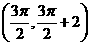 是直线
是直线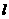 与曲线
与曲线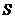 的一个切点;
的一个切点;
所以直线l与曲线S相切且至少有两个切点;
对任意x∈R,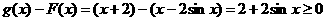 ,所以
,所以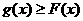
因此直线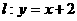 是曲线
是曲线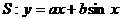 的“上夹线”.
的“上夹线”.
⑵推测: 的“上夹线”的方程为
的“上夹线”的方程为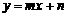
①先检验直线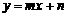 与曲线
与曲线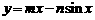 相切,且至少有两个切点:
相切,且至少有两个切点:
设:

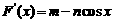 ,∴令
,∴令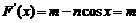 ,得:
,得: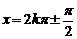 (k∈Z)
(k∈Z)
当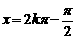 时,
时,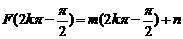 故:过曲线
故:过曲线 上的点(
上的点(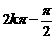 ,
,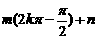 )的切线方程为:y-[
)的切线方程为:y-[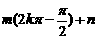 ]=
]= [
[ -(
-(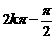 )],化简得:
)],化简得: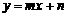 .
.
即直线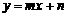 与曲线
与曲线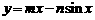 相切且有无数个切点.
相切且有无数个切点.
不妨设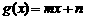 ②下面检验g(x)
②下面检验g(x)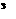 F(x)
F(x) g(x)-F(x)=
g(x)-F(x)= 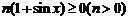 ∴直线
∴直线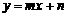 是曲线
是曲线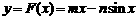 的“上夹线”.
的“上夹线”.
本资料由《七彩教育网》 提供!
20.解:(1)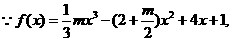
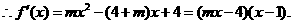
当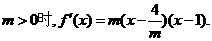 ①若
①若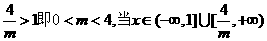 时有
时有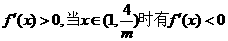
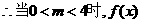 的单调递增区间为
的单调递增区间为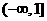 和
和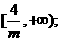
②若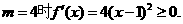
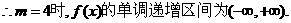
③若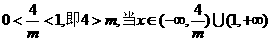 时有
时有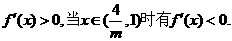

(2)当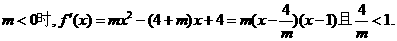

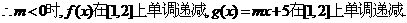
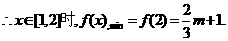
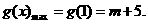 依题意
依题意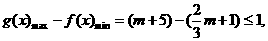 解得
解得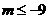 . 综上所述,存在
. 综上所述,存在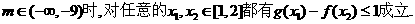
19. 解:(I)依题意,以
解:(I)依题意,以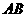 的中点
的中点 为原点建立直角坐标系
为原点建立直角坐标系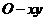 (如图),则点
(如图),则点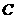 的横坐标为
的横坐标为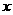 .
.
点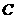 的纵坐标
的纵坐标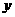 满足方程
满足方程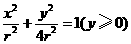 ,解得
,解得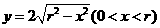
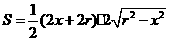
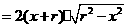 ,其定义域为
,其定义域为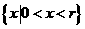 .
.
(II)记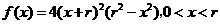 ,则
,则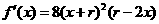 .
.
令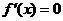 ,得
,得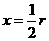 .因为当
.因为当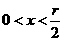 时,
时,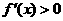 ;当
;当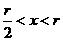 时,
时,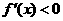 ,所以
,所以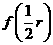 是
是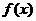 的最大值.因此,当
的最大值.因此,当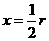 时,
时,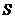 也取得最大值,最大值为
也取得最大值,最大值为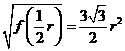 .
.
即梯形面积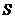 的最大值为
的最大值为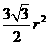 .
.
18.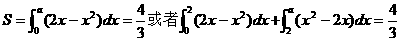
17.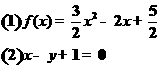
16.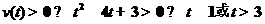
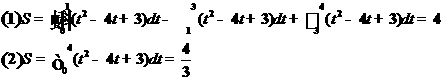
9: -16
;
10: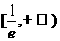 , 11:
, 11: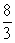 ; 12: 261.2(m) ;13:
; 12: 261.2(m) ;13: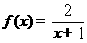 ;
;
14: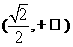 ;
15:
2 ;
-2 ;
;
15:
2 ;
-2 ;
21. 设直线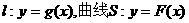 . 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有
. 若直线l与曲线S同时满足下列两个条件:①直线l与曲线S相切且至少有两个切点;②对任意x∈R都有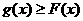 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
⑴已知函数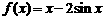 .求证:
.求证: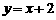 为曲线
为曲线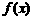 的“上夹线”.
的“上夹线”.
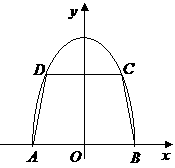
⑵观察下图:
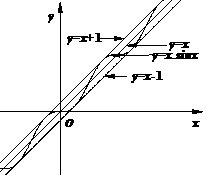
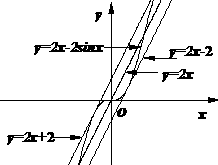
根据上图,试推测曲线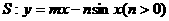 的“上夹线”的方程,并给出证明.
的“上夹线”的方程,并给出证明.
2009年衡阳市第八中学高二第一次月考数学(理科)参考答卷
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com