
题目列表(包括答案和解析)
4.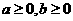 ,且
,且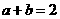 ,则( )
,则( )
A.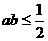 B.
B.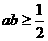 C.
C. 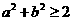 D.
D.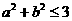
3.下列不等式成立的是( )
A.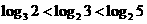 B.
B.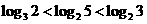
C.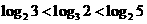 D.
D.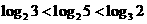
2.若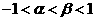 ,则下列各式中恒成立的是( )
,则下列各式中恒成立的是( )
A.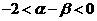 B.
B.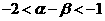 C.
C.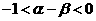 D.
D.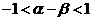
1.判断下列命题是否正确:(1)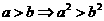 (2)
(2)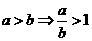 (3)
(3)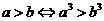
(4)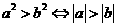 (5)
(5) 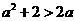 (6)
(6)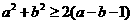 (7)
(7)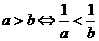
(8)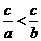 且
且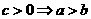 (9)
(9)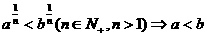
8.含参数不等式:
当遇到求解分歧时对参数分情况讨论;
不等式的恒成立问题:
(1)参数可分离型:变形为形如“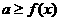 恒成立”;
恒成立”;
(2)参数不可分离型:常为二次形式不等式,如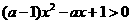
①若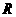 上恒成立,讨论步骤为
,
;(注意讨论二次项系数是否为0)
上恒成立,讨论步骤为
,
;(注意讨论二次项系数是否为0)
②若在小区间内恒成立,常用二次方程实根分布;从四方面限制 ,
, , ;
§6.5含绝对值的不等式
(1) 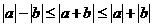 ,左右两个等号成立的条件分别为① ,②
;
,左右两个等号成立的条件分别为① ,②
;
(2)含绝对值不等式的证明方法:
利用不等式的性质、放缩法、换元法、反证法、基本不等式法.
基础练习:
7.指数和对数不等式:通常将不等式转化为以下两种形式
(1) 形如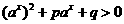 ,
,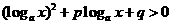 ;
;
(2)形如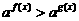 ,
,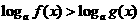 ;再利用函数的单调性求解.
;再利用函数的单调性求解.
注意:解对数不等式要求 (选“原式”或“转化后不等式”)的真数 0;
6.无理不等式:基本思想是“化成有理不等式”;
若能化成下列形式之一,可按等价的不等式组来求解:
(1)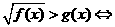 ,(2)
,(2)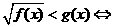 ,
,
(3)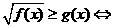 ,(4)
,(4)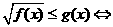 ,
,
其他情况: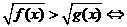 ,
,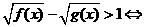 ;
;
5.含绝对值的不等式:基本思想是“去绝对值”;
(1)基本的绝对值不等式: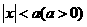 解集
,
解集
,
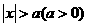 解集
;
解集
;
(2)含有两个或两个以上绝对值的绝对值不等式:常用“零点分段法”,注意分段的端点不重不漏;其它方法有平方法,有时可利用绝对值的几何意义;
(3)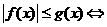 ,
,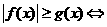 ;
;
4.一元分式不等式:
基本思想是“利用乘积的符号法则,将其转化为等价的 不等式”;
注意:(1)若分式两侧都非零,除非分母符号确定,否则应移项通分,
(2)若不等式带等号,其等价的不等式要加上分母不为零的限制条件;
3.一元高次不等式:解题步骤:(1)化为 因式的乘积(保证各项系数为正),(2)在序轴上标出各因式的零点,用“ 法”(原则: );
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com