
题目列表(包括答案和解析)
2.设随机变量n等可能地取值1,2,3,4,5,6,7,8,又设随机变量X=2n+1,则P(X<6)的值为( )
A.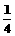 B.
B. 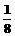 C.
C. 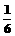 D.
D. 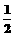
1.若直线的参数方程为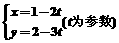 ,则直线的斜率为( )
,则直线的斜率为( )
A.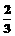 B.-
B.-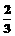 C.
C.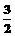 D.-
D.-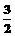
22.(本小题满分14分)某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
|
日 期 |
1月10日 |
2月10日 |
3月10日 |
4月10日 |
5月10日 |
6月10日 |
|
昼夜温差x(°C) |
10 |
11 |
13 |
12 |
8 |
6 |
|
就诊人数y(个) |
22 |
25 |
29 |
26 |
16 |
12 |
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程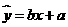 ;
;
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想? (参考公式: 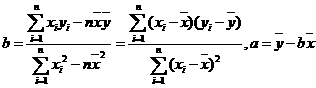 )
)
新泰一中08-09学年高二下学期期末考试
20. (本小题满分12分)设函数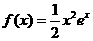 .
.
(1)求函数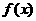 的单调区间;
的单调区间; 

(2)若当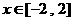 时,不等式恒
时,不等式恒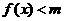 成立,求实数
成立,求实数 的取值范围.
的取值范围.
21(本小题满分12分).某商品,根据以往资料统计,顾客采用的付款期数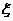 的分布列为
的分布列为
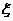 |
1 |
2 |
3 |
4 |
5 |
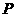 |
0.4 |
0.2 |
0.2 |
0.1 |
0.1 |
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.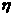 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(1)求事件 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率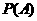 ;
;
(2)求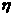 的分布列及期望
的分布列及期望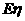 .
.
19. (本小题满分12分)已知数列{an}满足(n-1)an+1=(n+1)(an-1)且a2=6,
设bn=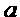 n+n(n∈N*).求{bn}的通项公式.
n+n(n∈N*).求{bn}的通项公式. 

18. (本小题满分12分)
已知函数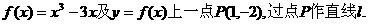


(1)求使直线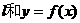 相切且以P为切点的直线方程;
相切且以P为切点的直线方程;
(2)求使直线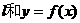 相切且切点异于P的直线方程
相切且切点异于P的直线方程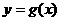 。
。
17.(本小题满分12分)
(1)已知复数z满足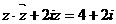 ,求复数z.
,求复数z. 

(2)已知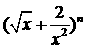 的展开式中,第5项的系数与第3项的系数之比是56:3,求展开式中的常数项。
的展开式中,第5项的系数与第3项的系数之比是56:3,求展开式中的常数项。
16.某商店要求甲、乙、丙、丁、戊五种不同的商品在货架上排成一排,其中甲、乙两种必须排在一起,而丙、丁两种不能排在一起,不同的排法共有 种.
15.观察下列各式9-1=8,16-4=12,25-9=16,
36-16=20…,这些等式反映了自然数间的某种规律,
设n表示自然数,用关于n的等式表示为 .
14.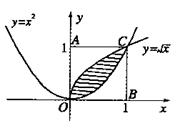 .曲线
.曲线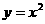 和曲线
和曲线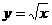 围成一个
围成一个
叶形图(如图所示阴影部分),其面积是______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com