
题目列表(包括答案和解析)
(1)已知全集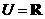 ,集合
,集合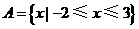 ,
,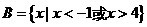 ,那么集合
,那么集合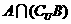 等于 ( )
等于 ( )
(A)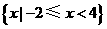 (B)
(B)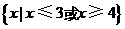
(C)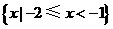 (D)
(D)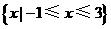
(2)复数(3+i)m-(2+i)对应的点在第三象限内,则实数m的取值范围是 ( )
(A)m< (B)m<1 ( C)<m<1 ( D)m>1
(3)直线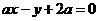 与圆
与圆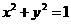 的位置关系是( )
的位置关系是( )
(A)相离 (B)相交 (C)相切 (D)不确定
(4)已知p:关于x的不等式x2+2ax-a>0的解集是R,q:-1<a<0,则p是q 的那么
(A)充分非必要条件 (B) 必要非充分条件
(C)
充要条件 (D) 既非充分又非必要条件 

(5)设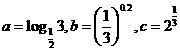 ,则()
,则()
A、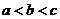 B、
B、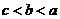 C、
C、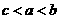 D、
D、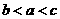
(6)甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为90人的样本,应在这三校分别抽取学生( )
(A)30人,30人,30人 (B)30人,45人,15人
(C)20人,30人,40人 (D)30人,50人,10人
(7)对于下列命题
①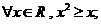 ②
②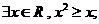 ③
③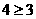 ;
;
④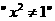 的充要条件是
的充要条件是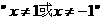 。
。 

其中正确命题的个数是
(A)0 (B)1 (C)2 (D)3
(8)函数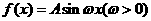 ,对任意
,对任意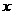 有
有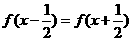 ,且
,且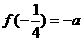 ,那么
,那么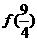 等于
等于
(A)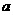 (B)
(B)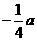 (C)
(C)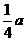 (D)
(D)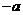
(9)若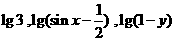 顺次成等差数列,则
顺次成等差数列,则
(A)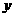 有最大值1,无最小值
(B)
有最大值1,无最小值
(B)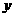 有最小值
有最小值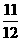 ,无最大值
,无最大值 

(C)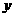 有最小值
有最小值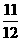 ,最大值1
(D)
,最大值1
(D)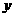 有最小值
有最小值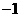 ,最大值1
,最大值1
(10)在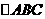 中,
中,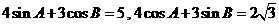 ,则角
,则角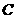 等于
等于
(A) (B)
(B)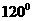 (C)
(C) (D)
(D)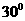
 (11)在平面直角坐标系
(11)在平面直角坐标系 中,设直线
中,设直线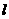 与抛物线
与抛物线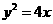 相交于
相交于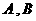 两点,给定下列三个条件:①
两点,给定下列三个条件:①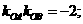 ②
②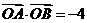 ; ③直线
; ③直线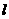 过定点(2,0)。如果将上面①、②、③中的任意一个作为条件,余下两个作为结论,则构成的三个命题中,真命题的个数是
过定点(2,0)。如果将上面①、②、③中的任意一个作为条件,余下两个作为结论,则构成的三个命题中,真命题的个数是
(A)3 (B)2 (C)1 (D)0
(12)已知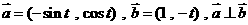 ,则
,则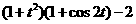 的值为
的值为
(A)1
(B)0 (C)5 (D)8


26.(本小题16分)在一次购物抽奖活动中,假设某10张奖券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;某顾客从此10张奖券中任抽2张,求:
(1)该顾客中奖的概率;
(2)求该顾客获奖的奖品总价值x(元)的概率分布列和数学期望E(x)。 

25.(本小题共15分)实力相等的甲、乙两名乒乓球选手进行比赛,规定5局3胜制(即5局内谁先赢3局就算获胜,并停止比赛)。
(1)试分别求甲打完3局、4局、5局才能获胜的概率; 

(2)求甲获胜的概率。
24.(本小题共15分)给定矩陈A=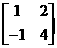 ,
B=
,
B=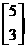 。
。
(1)求A的特征值λ1,λ2及对应的特征向量α1,α2;
(2)求A4B。 

23.(本小题16分)有4个不同的球,四个不同的盒子,现在要把球全部放入盒内。
(1)共有几种方法?
(2)恰有一个盒子不放球,共有几种方法?
(3)恰有一个盒子放2个球,共有几种方法? 

(4)恰有两个盒子不放球,共有几种方法?
22.(本小题共12分)设f(x)=(1+x)m+(1+x)n (m,n∈N*,且m,n≥2)展开式中x的系数是19。
(1)求f(x)展开式中x2的系数的最小值;
(2)对f(x)展开式中x2的系数取最小值时的m,
n,求f(x)展开式中x7的系数。 

21.(本小题共12分)A、B两个试验方案在某科学试验中成功的概率相同,已知A、B两个方案至少一个成功的概率为0.36。
(1)求两个方案均获成功的概率;
(2)设试验成功的方案个数为随机变量x,求x的概率分布列及数学期望E(x)。
20.(本小题12分)是否存在复数z,使其满足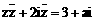 (a∈R)。如果存在,求复数z;如果不存在,说明理由。
(a∈R)。如果存在,求复数z;如果不存在,说明理由。
19.(本小题12分)在数列{an}中a1=1,an=2an-1+1 (n≥2)。
(1)求a2, a3, a4;
(2)猜想数列{an}的通项公式,并用数学归纳法来证明。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com