
题目列表(包括答案和解析)
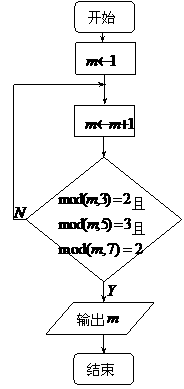

伪代码:
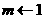
DO
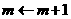
Loop Until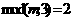 且
且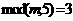 且
且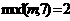
Print 
注:这里的解题的过程中运用的DO循环语句和课本上的解题略有区别请注意辨别!
“孙子问题”相当于求关于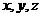 的不定方程组的
的不定方程组的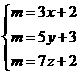 的正整数解;
的正整数解;
设所求的数为 ,根据题意
,根据题意 应该同时满足下列三个条件:
应该同时满足下列三个条件:
① 被3除后余2,即
被3除后余2,即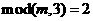 ;
;
② 被5除后余3,即
被5除后余3,即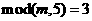 ;
;
③ 被7除后余2,即
被7除后余2,即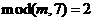 ;
;
用自然语言可以将算法写为:
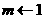
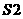
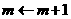
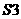 如果
如果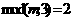 且
且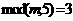 且
且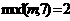 则执行
则执行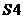 ,否则执行
,否则执行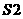 ;
;
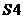 输出
输出
3.该问题的完整的表述,后来经过宋朝数学家秦九韶的推广,又发现了一种算法,叫做“大衍求一术”。在中国还流传着这么一首歌诀:
三人同行七十稀,
五树梅花廿一枝,
七子团圆月正半,
除百零五便得知。
它的意思是说:将某数(正整数)除以3所得的余数乘以70,除以5所得的余数乘以21,除以7所得的余数乘以15,再将所得的三个积相加,并逐次减去105,减到差小于105为止。 所得结果就是某数的最小正整数值。
用上面的歌诀来算《孙子算经》中的问题,便得到算式:
2×70+3×21+2×15=233,
 233-105×2=23,
233-105×2=23,
即所求物品最少是23件。
2.孙子算经的作者及确切的年代均不可考,不过根据考证,确切的年代不会在晋朝之後,以这个考证来说上面这种问题的解法,中国人发现得比西方早,所以这个问题的推广及其解法,被称为中国剩余定理。中国剩余定理(Chinese Remainder Theorem)在近代抽象代数学中占有一席非常重要的地位;
韩信是秦末汉初的著名军事家。据说有一次汉高祖刘邦在卫士的簇拥下来到练兵场,刘邦问韩信有什么方法,不要逐个报数,就能知道场上的士兵的人数。
韩信先令士兵排成3列纵队,结果有2个人多余;接着立即下令将队形改为5列纵队,这一改,又多出3人;随后他又下令改为7列纵队,这次又剩下2人无法成整行。
在场的人都哈哈大笑,以为韩信不能清点出准确的人数,不料笑声刚落,韩信高声报告共有士兵2333人。众人听了一愣,不知道韩信用什么方法这么快就能得出正确的结果的。同学们,你知道吗?
背景说明:
1.类似的问题最早出现在我国的《算经十书》之一的《孙子算经》中原文是:“今有物,不知其数,三三数之,剩二,五五数之,剩三,七七数之,剩二,问物几何?答曰:「二十三」”
⒐用三条直线x+2y-2=0,2x+y-2=0,x-y-3=0围成一个三角形,试写出三角形内部区域满足的不等式组.
⒍设x、y满足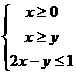 ,则z=3x+2y的最大值是
.
,则z=3x+2y的最大值是
.
⒈点P(a,3)到直线4x-3y+1=0的距离为4,且在不等式2x+y<3表示的平面区域内,则a的值是( )
A.-3 B.3 C.7 D.-7
⒉已知a>0,点集S的点(x,y)满足下列所有条件:①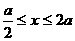 ,②
,②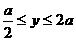 ,③
,③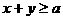 ,④
,④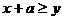 ,⑤
,⑤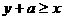 .则S的边界是一个有几条边的多边形( )
.则S的边界是一个有几条边的多边形( )
A.4 B.5 C.6 D.7
7、求证:若一个三角形的两条边不相等,则这两条边所对的角也不相等.
6、 用反证法证明命题“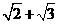 是无理数”时,假设正确的是( )
是无理数”时,假设正确的是( )
A.假设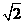 是有理数
B.假设
是有理数
B.假设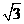 是有理数
是有理数
C.假设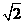 或
或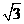 是有理数 D.假设
是有理数 D.假设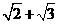 是有理数
是有理数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com