
题目列表(包括答案和解析)
1.函数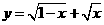 的定义域为( )
的定义域为( )
A.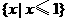 B.
B.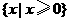
C.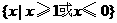 D.
D.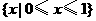
22.设数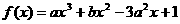
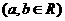 在
在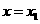 ,
,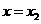 处取得极值,且
处取得极值,且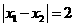 .
.
(1)若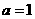 ,求
,求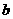 的值,并求
的值,并求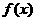 的单调递增区间;
的单调递增区间;
(2)若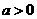 ,求
,求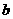 的取值范围.
的取值范围.

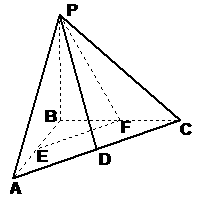
21.如图,在三棱锥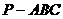 中,
中,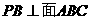 ,
,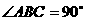 ,
,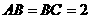 ,
,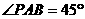 ,点
,点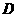 、
、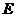 、
、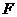 分别为
分别为 、
、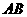 、
、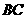 的中点。
的中点。
(1)求直线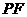 与平面
与平面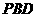 所成角的正弦值;
所成角的正弦值;
(2)求二面角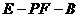 的正切值。
的正切值。

20.袋子 和
和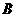 中装有若干个均匀的红球和白球,从
中装有若干个均匀的红球和白球,从 中摸出一个红球的概率是
中摸出一个红球的概率是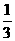 ,从
,从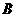 中摸出一个红球的概率为
中摸出一个红球的概率为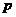 .
.
(1)从 中有放回地摸球,每次摸出一个,共摸4次.
中有放回地摸球,每次摸出一个,共摸4次.
①求恰好有2次摸到红球的概率;
②求第一次、第三次摸到红球的概率;
(2)若 、
、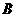 两个袋子中的球数之比为4,将
两个袋子中的球数之比为4,将 、
、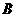 中的球装在一起后,从中摸出一个红球的概率是
中的球装在一起后,从中摸出一个红球的概率是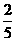 ,求
,求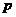 的值.
的值.
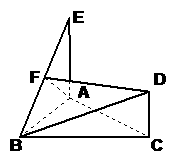
19.如图所示,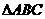 是正三角形,
是正三角形,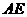 和
和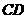 都垂直于平面
都垂直于平面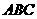 ,且
,且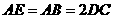 ,
,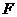 是
是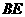 的中点。求证:(1)
的中点。求证:(1)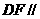 平面
平面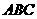 ;(2)
;(2)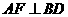
18.
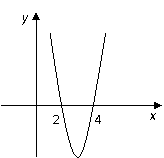 已知函数f (x)=ax3+bx2+cx在x0处取得极大值20,其导函数y=
已知函数f (x)=ax3+bx2+cx在x0处取得极大值20,其导函数y=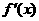 的图象经过点(2,0),(4,0),如右图所示:
的图象经过点(2,0),(4,0),如右图所示:
⑴ 求x0的值;
⑵ 求a,b,c的值。
17.在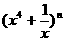 的展开式中,第三项的二项式系数比第二项的二项式系数大35。
的展开式中,第三项的二项式系数比第二项的二项式系数大35。
(1)求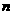 的值;
的值;
(2)求展开式中的常数项。
16.将正方形ABCD沿对角线BD折成直二面角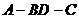 ,有如下四个结论:
,有如下四个结论:
①AC⊥BD;②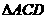 是等边三角形;③
是等边三角形;③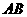 与
与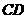 所成的角为
所成的角为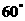 ;④
;④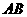 与平面
与平面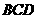 成
成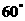 的角。其中正确的结论的序号是 。
的角。其中正确的结论的序号是 。
15.设曲线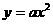 在点(1,
在点(1,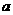 )处的切线与直线
)处的切线与直线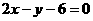 平行,则
平行,则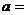 。
。
14.某学校共有师生2400人,现用分层抽样的方法,从所有师生中抽取一个容量为160的样本,已知从学生中抽取的人数为150,那么该学校的教师人数是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com