
题目列表(包括答案和解析)
9.已知空间向量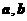 满足条件:
满足条件: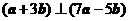 ,且
,且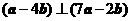 ,则空间
,则空间
向量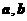 的夹角
的夹角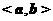 ( ▲ )
( ▲ )
A.等于 B.等于
B.等于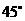 C.等于
C.等于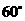 D.不确定
D.不确定
8.已知点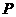 是抛物线
是抛物线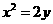 上的一动点,
上的一动点,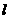 为准线,过点
为准线,过点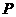 作直线
作直线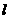 的垂线,垂足为
的垂线,垂足为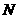 ,
,
已知定点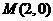 ,则当点
,则当点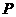 在该抛物线上移动时,
在该抛物线上移动时,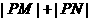 的最小值等于( ▲ )
的最小值等于( ▲ )
A.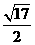 B.
B.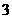 C.
C.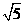 D.
D.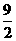
7.与命题:“若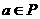 ,则
,则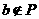 ”等价的命题是
( ▲ )
”等价的命题是
( ▲ )
A.若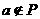 ,则
,则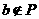 B.若
B.若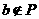 ,则
,则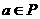
C.若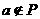 ,则
,则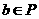 D.若
D.若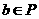 ,则
,则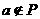
6.已知双曲线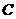 的焦点、实轴端点分别恰好是椭圆
的焦点、实轴端点分别恰好是椭圆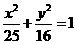 的长轴端点、焦点,则双
的长轴端点、焦点,则双
曲线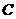 的渐近线方程为
( ▲ )
的渐近线方程为
( ▲ )
A.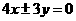 B.
B.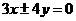 C.
C.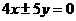 D.
D.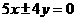
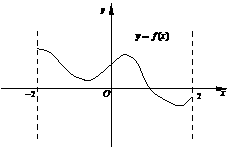
5.函数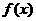 在
在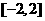 内的图象如图所示,若函数
内的图象如图所示,若函数
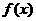 的导函数
的导函数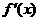 的图象也是连续不间断的,则
的图象也是连续不间断的,则
导函数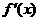 在
在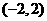 内有零点
( ▲ )
内有零点
( ▲ )
A. 个
B.
个
B.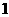 个
个
C.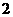 个 D.至少
个 D.至少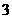 个
个
4.下列命题中是真命题的为 ( ▲ )
A. ,
,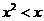 B.
B. ,
,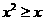
 C.
C.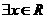 ,
,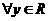 ,
,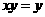 D.
D. ,
,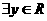 ,
,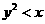
3.已知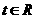 ,
,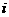 为虚数单位,若复数
为虚数单位,若复数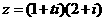 是纯虚数,则
是纯虚数,则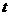 的值等于 ( ▲ )
的值等于 ( ▲ )
A.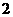 B.
B.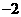 C.
C.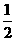 D.
D.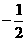
2.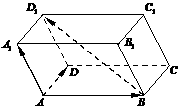 如图,在平行六面体
如图,在平行六面体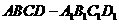 中,已知
中,已知
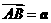 ,
,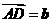 ,
,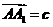 ,则用向量
,则用向量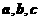 可表
可表
示向量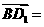 ( ▲ )
( ▲ )
A.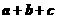 B.
B.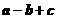
C.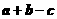 D.
D.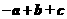
有一项是符合题目要求的.
1.设复数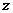 满足
满足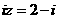 (
(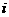 为虚数单位),则
为虚数单位),则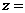 ( ▲ )
( ▲ )
A.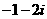 B.
B.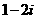 C.
C.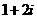 D.
D.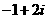
22. (本小题满分12分) 已知定义在正实数集上的函数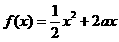 ,
,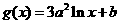 ,其中
,其中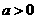 .设两曲线
.设两曲线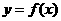 ,
,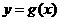 有公共点,且在该点处的切线相同.
有公共点,且在该点处的切线相同.
(I)用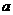 表示
表示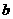 ,并求
,并求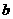 的最大值;(II)求证:
的最大值;(II)求证: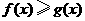 (
(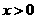 ).
).
本小题主要考查函数、不等式和导数的应用等知识,考查综合运用数学知识解决问题的能力.
解:(Ⅰ)设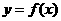 与
与 在公共点
在公共点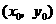 处的切线相同.
处的切线相同.
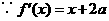 ,
,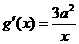 ,由题意
,由题意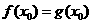 ,
,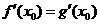 .
.
即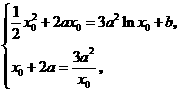 由
由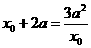 得:
得: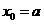 ,或
,或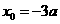 (舍去).
(舍去).
即有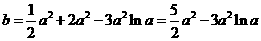 .
.
令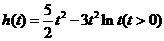 ,则
,则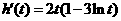 .于是
.于是
当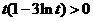 ,即
,即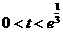 时,
时,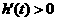 ;
;
当 ,即
,即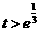 时,
时,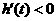 .
.
故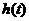 在
在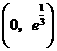 为增函数,在
为增函数,在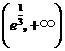 为减函数,
为减函数,
于是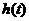 在
在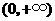 的最大值为
的最大值为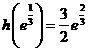 .
.
(Ⅱ)设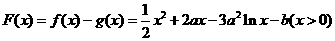 ,
,
则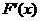
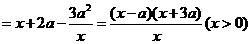 .
.
故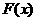 在
在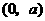 为减函数,在
为减函数,在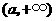 为增函数,
为增函数,
于是函数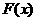 在
在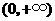 上的最小值是
上的最小值是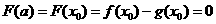 .
.
故当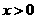 时,有
时,有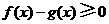 ,即当
,即当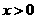 时,
时,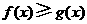 .
.
21解:设该工人在2006年一年里所得奖金为X,则X是一个离散型随机变量.由于该工人每季度完成任务与否是等可能的,所以他每季度完成任务的概率等于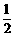 ,所以,
,所以,
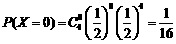 ,
,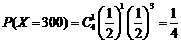 ,
,
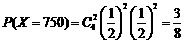 ,
,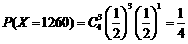 ,
,
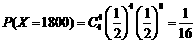 .
.
 其分布列为
其分布列为
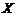 |
0 |
300 |
750 |
1260 |
1800 |
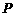 |
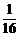 |
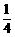 |
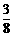 |
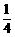 |
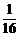 |

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com