
题目列表(包括答案和解析)
21.(12分)设函数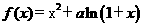 有两个极值点
有两个极值点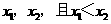 。
。
(1):求a的取值范围,并讨论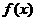 的单调性;
的单调性;
(2):证明: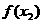
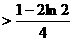 。
。
2009年重庆一中高2010级期末考试(本部)
20.(12分)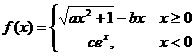 其中
其中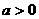
(1)若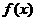 在R上连续,求
在R上连续,求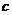
(2)若要使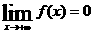 ,则
,则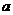 与
与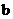 应满足哪些条件?
应满足哪些条件?
(3)若对于任意的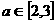 ,
,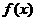 是
是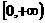 的单调减函数,求
的单调减函数,求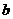 的范围。
的范围。
19.(12分)设正数数列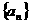 为等比数列,
为等比数列,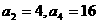 。
。
(1)求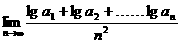
(2)记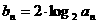 ,证明: 对任意的
,证明: 对任意的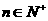 ,有
,有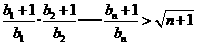 成立.
成立.
18.(13分)函数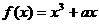 与
与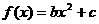
(1)若点 是函数与
是函数与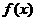 与
与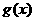 的图象的一个公共点,且两函数的图象在点
的图象的一个公共点,且两函数的图象在点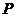 处有
处有
相同的切线,求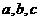
(2)若函数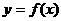 点
点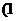 ,
,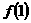 )处的切线为
)处的切线为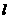 ,若
,若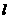 与圆C:
与圆C: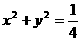 相切,求
相切,求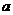 的值.
的值.
17.(13分)某人在自己的经济林场种植了杨树、沙柳等植物。一次种植了n株沙柳,各株沙柳成活与否是相互独立的,成活率为p,设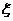 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望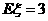 ,标准差
,标准差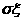 为
为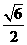 。
。
(1)求n,p的值
(2)若一株沙柳成活,则一年内通过该株沙柳获利100元,若一株沙柳不能成活,一年内通过该株沙柳损失30元,求一年内该人通过种植沙柳获利的期望
16.(13分)一个布袋里有3个红球,2个白球共5个球. 现抽取3次,每次任意抽取2个,并待放回后再抽下一次,求:
(1)3次抽取中,每次取出的2个球都是1个白球和1个红球的概率;
(2)3次抽取中,有2次取出的2个球是1个白球和1个红球,还有1次取出的2个球同色的概率;
15.下列说法正确的有:
(1)若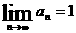 ,则当
,则当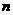 足够大时,
足够大时,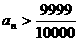
(2)由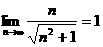 可知
可知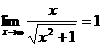
(3)若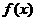 是偶函数且可导,则
是偶函数且可导,则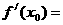
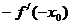
(4)若函数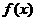 中,
中,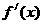 与
与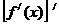 都存在,且
都存在,且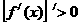 ,
,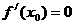 ,则
,则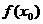 是函数
是函数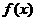 的一个极小值。
的一个极小值。
三解答题(共75分)
14.已知函数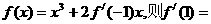 .
.
13.若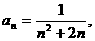 则
则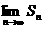 .
.
12.若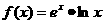 ,则
,则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com