
题目列表(包括答案和解析)
1.分类计数原理:做一件事情,完成它可以有n类办法,在第一类办法中有m1种不同的方法,在第二类办法中有m2种不同的方法,……,在第n类办法中有mn种不同的方法 那么完成这件事共有
那么完成这件事共有
N=m1+m2+……+mn 种不同的方法
1理解分类计数原理与分步计数原理,并能用它们分析和解决一些简单的应用问题;
2.理解排列的意义;掌握排列数计算公式,并能用它解决一些简单的应用问题.
5.例题思考:
例1:①利用差角余弦公式求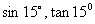 的值
的值
②利用和角余弦公式求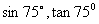 的值
的值
例2:已知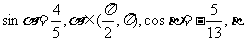 是第三象限角,求
是第三象限角,求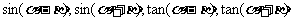 的值。
的值。
例3.计算下列各式的值
①
②
③
④
例4.化简:①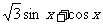 ,
②
,
②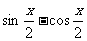
例5.已知:sin
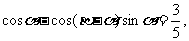 β是第三象限角,求
β是第三象限角,求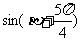 ,tan(
,tan(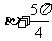 )的值
)的值
4.知识点小结:sin(α+β)= sin(α-β)
tan(α+β)= tan(α-β)=
3.思考并回答以下问题:
(1)诱导公式(五)的内容是什么
(2) 诱导公式(六)的内容是什么
(3)sin(α+β)=cos( )= cos ( )cos( ) sin( )sin( )
化简得 sin(α+β)=
sin(α-β)=
由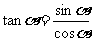 你能推倒出tan(α+β)=
你能推倒出tan(α+β)=
2.自学内容:通读教材128页倒数第三行_行至131页14行,约用10分钟。
1.学习目标:两角差与和的正弦公式和正切公式的应用
10.如果在(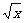 +
+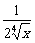 )n的展开式中,前三项系数成等差数列,求展开式中的有理项.
)n的展开式中,前三项系数成等差数列,求展开式中的有理项.
8. (2005广东)已知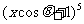 的展开式中
的展开式中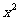 的系数与
的系数与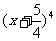 的展开式中x3的系数相等,则
的展开式中x3的系数相等,则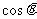 =
.
=
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com