
题目列表(包括答案和解析)
3.抛物线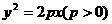 的几何性质:
的几何性质:
(1)范围
因为p>0,由方程可知x≥0,所以抛物线在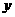 轴的右侧,
轴的右侧,
当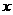 的值增大时,|
的值增大时,|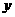 |也增大,说明抛物线向右上方和右下方无限延伸.
|也增大,说明抛物线向右上方和右下方无限延伸.
(2)对称性:对称轴要看一次项,符号决定开口方向.
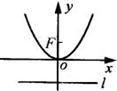
(3)顶点(0,0),离心率: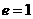 ,焦点
,焦点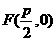 ,准线
,准线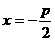 ,焦准距p.
,焦准距p.
(4) 焦半径:抛物线
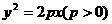 上一点
上一点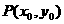 到焦点
到焦点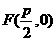 的距离
的距离 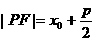
抛物线 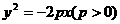 上一点
上一点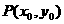 到焦点
到焦点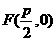 的距离
的距离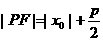
抛物线 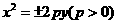 上一点
上一点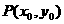 到焦点
到焦点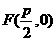 的距离
的距离 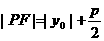
(5) 焦点弦:抛物线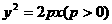 的焦点弦
的焦点弦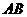 ,
,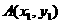 ,
,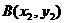 ,则
,则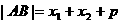 .
.
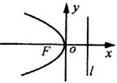
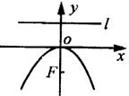
2.抛物线四种标准方程的几何性质:
|
标准方程 |
图形 |
顶点 |
对称轴 |
焦点 |
准线 |
离心率 |
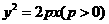 |
 |
 |
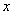 轴 轴 |
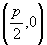 |
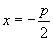 |
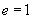 |
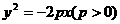 |
 |
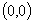 |
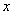 轴 轴 |
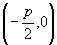 |
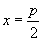 |
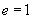 |
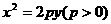 |
 |
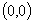 |
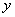 轴 轴 |
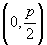 |
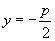 |
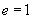 |
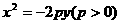 |
 |
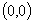 |
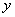 轴 轴 |
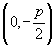 |
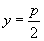 |
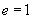 |
1.抛物线定义:平面内到一定点F和一条定直线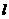 的距离相等的点的轨迹称为抛物线.
的距离相等的点的轨迹称为抛物线.
1、在等差数列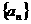 中,若共有奇数项 中,若共有奇数项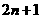 项,则 项,则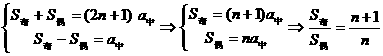 |
|
2、在等差数列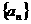 中,若a1>0, 中,若a1>0,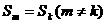 ,则①m、k同奇或同偶时, ,则①m、k同奇或同偶时,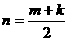 时, 时,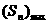 ②当m、k-奇-偶时, ②当m、k-奇-偶时,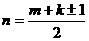 时 时 |
|
3、等差数列中,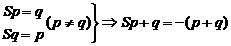 (用多种方法证,如 (用多种方法证,如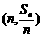 共线等) 共线等) |
|
4、等差数列中,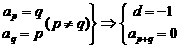 |
|
5、等差数列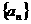 、 、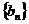 中,有 中,有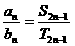 如C95等差数列 如C95等差数列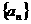 、 、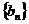 的前n项和分别为 的前n项和分别为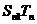 ,若 ,若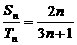 ,求 ,求 |
|
6、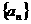 为等差数列, 为等差数列,其前n项和为 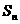 ,求 ,求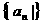 的前n项和 的前n项和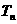 |
⑴a1>0,d<0时,则数列为减,设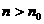 时, 时,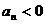 , ,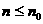 时, 时,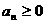 则: 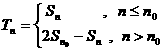 |
⑵a1<0,d>0时,数列为增,设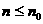 时, 时,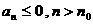 时 时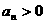 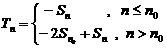 如 如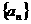 的前n项和 的前n项和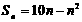 ,求 ,求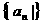 |
|
|
等差数列 |
等比数列 |
|
定义 |
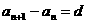 常数 常数 |
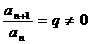 的常数 的常数 |
|
通项 公式 |
①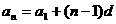 ② 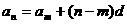 ③叠加: 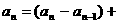 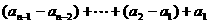 |
①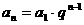 ② 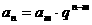 ③叠乘: 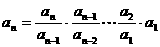 |
|
增 减 性 |
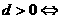 递增 递增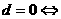 常数列 常数列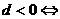 递减 递减 |
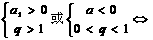 递增 递增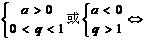 递减 递减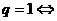 常数列 常数列 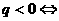 摆动数列 摆动数列 |
|
前 n 项 和 |
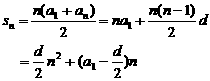 推导方法:倒序相加 |
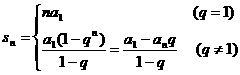 推导方法:乘公比错位相减 |
|
中 项 |
A为a、b的等差中项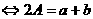 推广:2 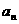 = =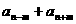 |
G为a、b的等比中项 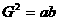 推广: 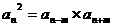 |
|
性 质 |
⑴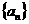 为等差数列 为等差数列 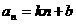 (k、b常数) ⑵ 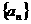 为等差数列 为等差数列 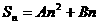 ⑶ 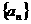 为等差数列,若 为等差数列,若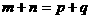 则 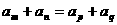 ⑷ 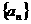 为等差数列, 为等差数列,则 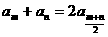 (m,n同奇或同偶) ⑸ 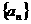 为等差数列, 为等差数列,则 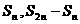 , ,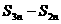 成等差数列 成等差数列(6) 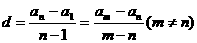 |
⑴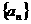 为等比数列, 为等比数列,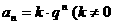 , ,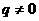 ) )⑵ 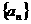 为等比数列,且 为等比数列,且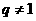 , ,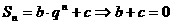 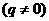 ⑶ 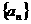 为等比数列,若 为等比数列,若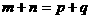 , ,则 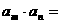 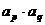 ⑷ 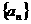 为等差数列,则 为等差数列,则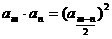 ⑸ 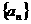 为等比数列, 为等比数列,则 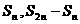 , ,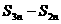 成等比数列 成等比数列(6) 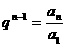 , ,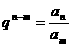 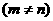 |
5.椭圆系方程:
与椭圆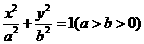 共焦点的椭圆系方程可设为:是
共焦点的椭圆系方程可设为:是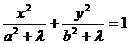 (
(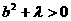 ).
).
与椭圆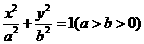 有相同离心率的椭圆系方程可设为:
有相同离心率的椭圆系方程可设为: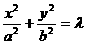 或
或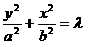 .
.
4.椭圆的的内外部:
(1)点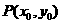 在椭圆
在椭圆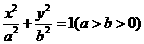 的内部
的内部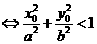
(2)点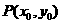 在椭圆
在椭圆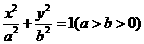 的外部
的外部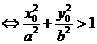
3.椭圆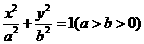 的性质:
的性质:
(1)范围: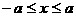 ,
,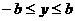
(2)对称性:关于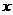 轴、
轴、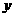 轴、原点对称
轴、原点对称
(3)顶点坐标、焦点坐标是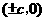
(4)长轴长2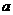 、短轴长2
、短轴长2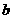 、焦距2c、长半轴
、焦距2c、长半轴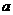 、短半轴
、短半轴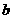 、半焦距
、半焦距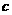
(5)椭圆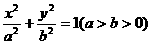 的,准线方程是
的,准线方程是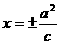 ,准线到中心的距离为
,准线到中心的距离为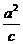 .
.
通径的长是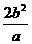 ,通径的一半(半通径):
,通径的一半(半通径):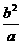 ,焦准距(焦点到对应准线的距离)
,焦准距(焦点到对应准线的距离)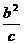 .
.
(6)离心率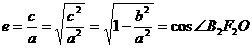 ,离心率越大,椭圆越扁
,离心率越大,椭圆越扁
(7)焦半径:若点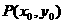 是椭圆
是椭圆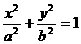
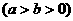 上一点,
上一点, 是其左、右焦点,
是其左、右焦点,
焦半径的长: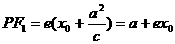 和
和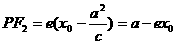 .
.
2.椭圆的标准方程:焦点在 轴上时,方程为
轴上时,方程为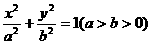 焦点
焦点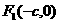
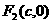
焦点在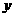 轴上时,方程为
轴上时,方程为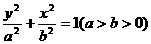 焦点
焦点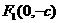
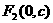
注: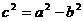
 椭圆的一般方程:
椭圆的一般方程: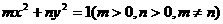
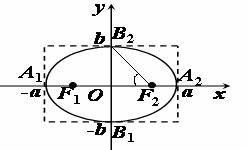
1.椭圆定义:一个动点P,平面内与两定点F1,F2的距离的和等于常数
(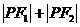 =2
=2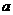 (
(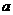 为常数)2
为常数)2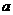 >
>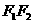 )的点的轨迹叫做椭圆.
)的点的轨迹叫做椭圆.
⑴若2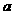 >
>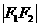 ,则动点P的轨迹是椭圆
,则动点P的轨迹是椭圆
⑵若2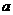 =
=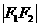 ,则动点P的轨迹是线段F1F2
,则动点P的轨迹是线段F1F2
⑶若2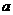 <
<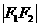 ,则动点P无轨迹
,则动点P无轨迹
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com