
题目列表(包括答案和解析)
5.(2006全国Ⅰ)安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有__________种 (用数字作答)
(用数字作答)
4.已知集合A={5},B={1,2},C={1,3,4},从这三个集合中各取一个元素构成空间直角坐标系中点的坐标,则确定的不同点的个数为
(A)33 (B)34 (C)35 (D)36
3. 6个人并排站成一排,B站在A的右边,C站在B的右边,则不同的排法总数为
A. 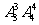 B.
B. 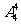 C.
C. 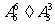 D.
D. 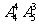 ( )
( )
2.若2n个学生排成一排的排法数为x,这2n个学生排成前后两排,每排各n个学生的排法数为y,则x、y的关系为 ( )
A.x>y B.x<y C.x=y D.x=2y
1.从长度分别为1、2、3、4的四条线段中,任取三条的不同取法共有n种,在这些取法中,以取出的三条线段为边可组成的三角形的个数为m,则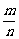 等于 ( )
等于 ( )
A.0 B.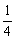 C.
C.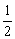 D.
D.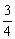
[例1]从集合{1,2,3,…,10}中,选出由5个数组成的子集,使得这5个数中的任何两个数的和不等于11,这样的子集共有多少个?
[例2]二次函数y=ax2+bx+c的系数a、b、c,在集合{-3,-2,-1,0,1,2,3,4}中选取3个不同的值,则可确定坐标原点在抛物线内部的抛物线多少条?
[例3]有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?
(1)甲不在中间,乙必在两端;
(2)甲不在左端,乙不在右端;
(3)男、女生分别排在一起;
(4)男女相间;
(5)甲、乙、丙三人从左到右顺序保持一定.
[例4]用0~9这十个数字组成没有重复数字的正整数
(1)共有几个三位数?
(2)求所有三位数的和;
(3)能被4整除的三位数有多少?
(4)比5231大的四位数有多少?
5.带限制条件排列问题
(1)限制条件的常见类型及解法:
某元素在不在某位置--优先按排受限制的元素或位置;
元素相邻--捆绑法,即把相邻元素看成一个元素;
元素不相邻--插空法;
数的大小,先考虑首位或前几位;整除问题,先看末位;
(2)一般思想方法:直接法,间接法,排除法,优先安排特殊元素或位置.务必做到分步清楚,分类明确,不重不漏.
4.排列:从n个不同的元素中取出m个(m≤n)元素并按一定的顺序排成一列,叫做从n个不同元素中取出m个元素的一个排列.
(1)排列数: 从n个不同的元素中取出m个(m≤n)元素的所有排列的个数.
(2)排列数公式: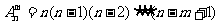
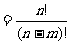 .
.
Ann=n!=n(n-1)! 规定 0!=1
3.两个计数原理的区别:
如果完成一件事,有n类办法,不论哪一类办法中的哪一种方法,都能独立完成这件事,用分类计数原理,
如果完成一件事需要分成几个步骤,各步骤都不可缺少,需要完成所有步骤才能完成这件事,是分步问题,用分步计数原理.
两个计数原理用来计算完成一件事的不同方法种数的,是计算排列组合,概率统计的基础,在生产,生活及科学实验中有广泛的应用.
2.分步计数原理:做一件事情,完成它需要分成n个步骤,做第一步有m1种不同的方法,做第二步有m2种不同的方法,……,做第n步有mn种不同的方法,那么完成这件事有N=m1×m2×……mn 种不同的方法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com