
题目列表(包括答案和解析)
21.(本小题满分10分)已知函数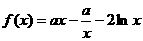 在其定义域内为单调函数,求
在其定义域内为单调函数,求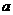 的取值
的取值
范围.
解: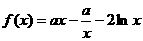 的定义域为
的定义域为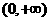 ,则
,则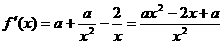 .
.
令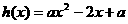 (
(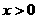 ),
),
①当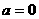 时,
时,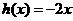 ,因为
,因为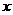 >
> ,所以
,所以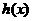 <0,
<0,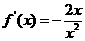 <0,
<0,
∴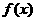 在
在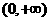 内是单调递减函数,即
内是单调递减函数,即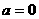 符合题意;
符合题意;
②当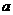 >0时,
>0时,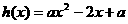 的图像为开口向上的抛物线,对称轴为
的图像为开口向上的抛物线,对称轴为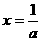 ,而
,而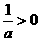 ,
,
∴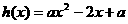 在
在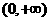 内有最小值
内有最小值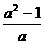 ,
,
只需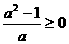 ,即
,即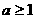 时,
时,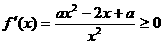 .
.
∴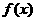 在
在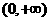 内为单调递增函数,故
内为单调递增函数,故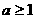 .
.
③当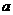 <0时,
<0时,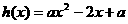 的图像为开口向下的抛物线,对称轴为
的图像为开口向下的抛物线,对称轴为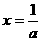 ,而
,而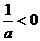 ,∴
,∴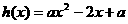 在
在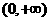 内单调递减,只要
内单调递减,只要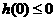 ,即
,即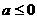 时,
时,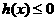 在
在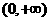 内恒成立,此时,
内恒成立,此时,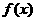 在
在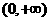 内是减函数,故
内是减函数,故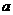 <0符合题意.
<0符合题意.
综上所述,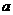 的取值范围是
的取值范围是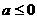 或
或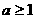 .
.
20.(本小题满分10分)在三棱锥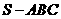 中,△
中,△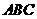 是边长为
是边长为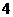 的正三角形,平面
的正三角形,平面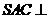 平面
平面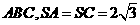 ,
,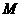 、
、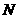 分别为
分别为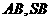 的中点.
的中点.
(1)证明: ⊥
⊥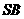 ;
;
(2)求二面角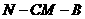 的余弦值.
的余弦值.
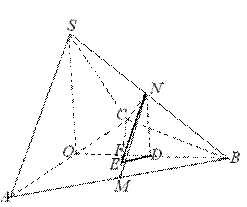 解法1:(1)连接S与AC的中点O,因为SA=SC,所以
解法1:(1)连接S与AC的中点O,因为SA=SC,所以
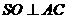 ,因为平面
,因为平面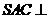 平面
平面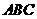 ,
,
 平面
平面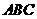 .连接BO, 则BO为SB在平面
.连接BO, 则BO为SB在平面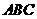 内的射影.
内的射影.
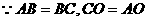 ,
,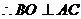 ,
,
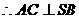 .
.
(2)连接N与BO的中点D, 则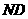 ∥SO,
∥SO,
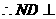 平面CMB.
平面CMB.
过D作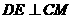 于点E, 连接NE,
于点E, 连接NE,
则∠NED即为所求二面角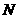 -
-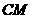 -
-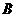 的平面角.
的平面角.
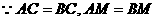 ,
, ∥BM. 设BO与CM交点为F, 则F为△
∥BM. 设BO与CM交点为F, 则F为△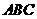 的重心.
的重心.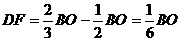 ,
,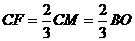 ,
,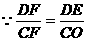 ,
,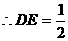 ,
,
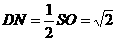 ,
,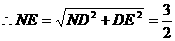 ,
,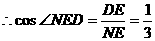 .
.
 解法2: 连接S与AC的中点O,因为SA=SC,所以
解法2: 连接S与AC的中点O,因为SA=SC,所以
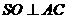 ,因为平面
,因为平面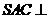 平面
平面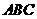 ,
,
 平面
平面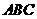 .
.
连接BO, 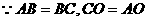 ,
,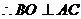 . 如图,以O为坐标原点,分别以OA,OB,OS所在直线为
. 如图,以O为坐标原点,分别以OA,OB,OS所在直线为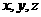 轴建系. 则
轴建系. 则
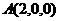 ,
,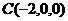 ,
,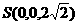 ,
,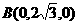 ,
,
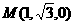 ,
,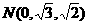 .
.
(1)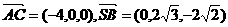 ,
,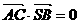 ,
,
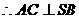 .
.
(2)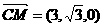 ,
,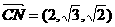 ,设平面CMN的法向量为
,设平面CMN的法向量为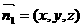 ,则
,则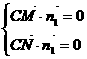 ,所以平面CMN的一个法向量为
,所以平面CMN的一个法向量为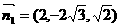 ,平面CMB的一个法向量为
,平面CMB的一个法向量为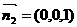 .
.
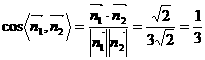 . 所以二面角
. 所以二面角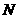 -
-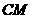 -
-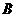 平面角的余弦值为
平面角的余弦值为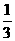 .
.
19.(本小题满分8分)已知直线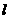 过定点
过定点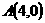 ,且与抛物线
,且与抛物线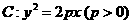 交于
交于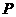 、
、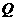 两点,若以
两点,若以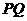 为直径的圆经过原点
为直径的圆经过原点 ,求抛物线的方程.
,求抛物线的方程.
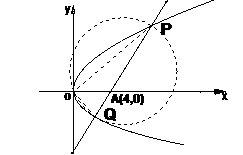 解:可设直线
解:可设直线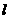 的方程为
的方程为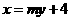 代入
代入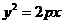 ,
,
得 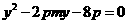 设
设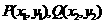 ,
,
则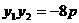 ,
,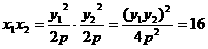
由题意知,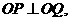 则
则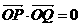 ,
,
即 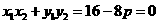 ,
,
∴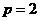 , 此时,抛物线的方程为
, 此时,抛物线的方程为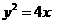
18.(本小题满分8分)设函数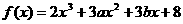 在
在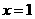 及
及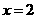 时取得极值.
时取得极值.
(1)求a、b的值;
(2)求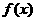 的单调区间.
的单调区间.
解:(1)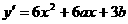 ,由已知,得
,由已知,得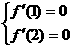 解得
解得
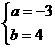
(2)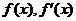 随
随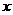 的变化情况如下表:
的变化情况如下表:
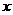 |
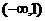 |
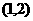 |
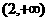 |
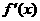 |
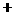 |
- |
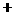 |
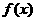 |
增 |
减 |
增 |
所以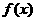 在
在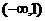 上是增函数,在
上是增函数,在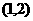 上为减函数,在
上为减函数,在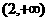 上是增函数.
上是增函数.
17.解法1:过E作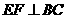 于点F,连接DF,则∠EDF即为直线DE与平面ABCD所成角.
于点F,连接DF,则∠EDF即为直线DE与平面ABCD所成角.
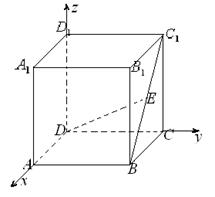 因为E为BC1的中点,所以F为BC的中点.
因为E为BC1的中点,所以F为BC的中点.
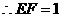 ,
,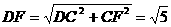 ,
,

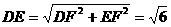 ,
,
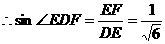 =
=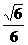 .
.
解法2:以D为坐标原点,分别以DA,DC,DD1
所在直线为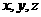 轴建系. 则
轴建系. 则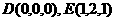 ,
,
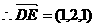 ,平面ABCD的法向量
,平面ABCD的法向量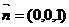 ,
,
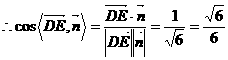 ,所以直线DE与平面ABCD所成角的正弦值为
,所以直线DE与平面ABCD所成角的正弦值为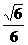 .
.
13.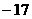 14.4
15.
14.4
15.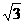 16.
16.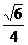
1.C 2.B 3.B 4.C 5.A 6.A 7.D 8.D 9.C 10.A 11.D 12.A
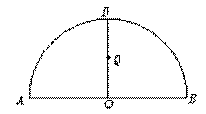
22.(本小题满分12分)如图,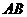 为半圆直径,
为半圆直径, 为半圆圆心,且
为半圆圆心,且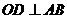 ,
,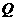 为线段
为线段 的中点,
的中点,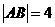 ,曲线
,曲线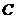 过点
过点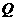 ,动点
,动点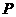 在曲线
在曲线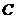 上运动,且保持
上运动,且保持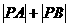 的值不变.
的值不变.
(1)建立适当的平面直角坐标系,求曲线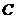 的方程;
的方程;
 (2)若过点
(2)若过点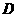 的直线
的直线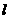 与曲线
与曲线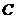 相交于不同的两点
相交于不同的两点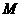 、
、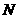 ,且点
,且点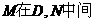 ,设
,设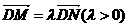 ,求
,求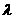 的取值范围.
的取值范围.
2008-2009学年
东北师大附中 高二数学(文科)试卷
下学期期末考试
命题人:王 生 田京爱 审题人:李晓松 2009-07-09
第Ⅰ卷(选择题 共48分)
21.(本小题满分10分)已知函数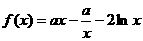 在其定义域内为单调函数,求
在其定义域内为单调函数,求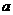 的取值
的取值
范围.
20. (本小题满分10分)在三棱锥
(本小题满分10分)在三棱锥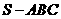 中,△
中,△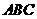 是边长为
是边长为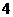 的正三角形,平面
的正三角形,平面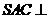 平面
平面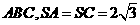 ,
,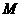 、
、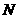 分别为
分别为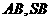 的中点.
的中点.
(1)证明: ⊥
⊥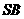 ;
;
(2)求二面角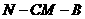 的余弦值.
的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com