
题目列表(包括答案和解析)
4.熟练掌握二项式定理的基本问题――通项公式及其应用
3.掌握二项式定理在近似计算及证明整除性中的应用
2.会区分项的系数与项的二项式系数
1.正确理解二项式定理,能准确地写出二项式的展开式
5.双曲线系方程
(1) 双曲线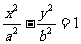 共焦点的双曲线系方程是
共焦点的双曲线系方程是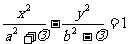 (
(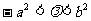 )
)
(2) 双曲线 共渐近线的双曲线系方程可设为
共渐近线的双曲线系方程可设为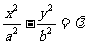
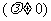 .
.
(当 时焦点在
时焦点在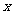 轴,当
轴,当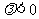 时焦点在
时焦点在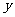 轴上).
轴上).
4.双曲线的内外部
(1) 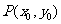 在双曲线
在双曲线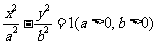 的内部
的内部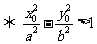 .
.
(2) 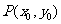 在双曲线
在双曲线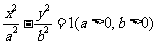 的外部
的外部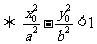 .
.
3.双曲线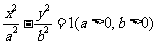 的性质:
的性质:
(1)范围: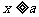 或
或 ,
,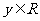 .
.
(2)对称性:关于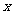 轴、
轴、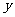 轴、原点对称.
轴、原点对称.
(3)顶点坐标:双曲线和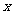 轴有两个交点
轴有两个交点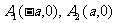 ,焦点坐标是
,焦点坐标是 .
.
(4)实轴长2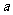 、虚轴长2
、虚轴长2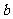 、焦距2
、焦距2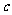 ;实半轴
;实半轴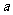 、虚半轴
、虚半轴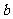 、半焦距
、半焦距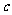 .
.
(5)双曲线 的准线方程是
的准线方程是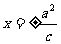 ,准线到中心的距离为
,准线到中心的距离为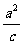 ,
,
焦准距:(焦点到对应准线的距离)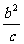 .
.
通径的长是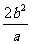 ,通径的一半(半通径):
,通径的一半(半通径):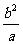 .
.
(6) 渐近线方程是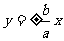
① 双曲线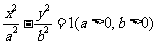 渐近线方程:令
渐近线方程:令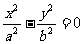
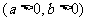 ,即
,即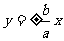 ;
;
② 渐近线是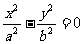 (或
(或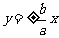
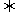
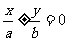 )的双曲线设为
)的双曲线设为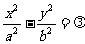 .
.
(λ≠0),k是待定系数.
③(焦渐距)焦点到渐近线的距离恒为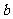 .
.
(7) 等轴双曲线:实轴和虚轴等长的双曲线叫做等轴双曲线. 定义式: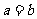 .
.
注:①等轴双曲线的渐近线方程为: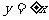 .②渐近线互相垂直.
.②渐近线互相垂直.
③等轴双曲线可设为: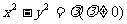 .(
.( 时焦点在
时焦点在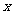 轴,
轴,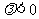 时焦点在
时焦点在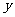 轴上)
轴上)
(8) 离心率是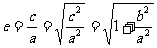 (
(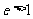 )
)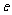 越大,开口越开阔;
越大,开口越开阔;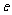 越小,开口越扁狭.
越小,开口越扁狭.
(9) 半径:若点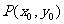 是双曲线
是双曲线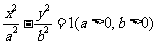 上一点,
上一点,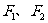 是其左、右焦点,
是其左、右焦点, 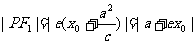 ,
, 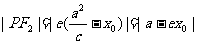
即焦半径:点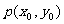 在左支上
在左支上 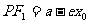 和
和 .
.
点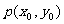 在右支上
在右支上 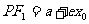 和
和 .
.
2.双曲线的标准方程:
焦点在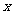 轴上时,方程为
轴上时,方程为
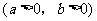 焦点
焦点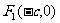
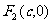
焦点在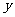 轴上时,方程为
轴上时,方程为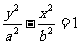
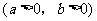 焦点
焦点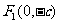
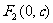
注: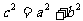 (类比勾股定理)
(类比勾股定理)
双曲线的一般方程: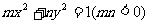
注:方程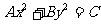 (
(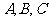 均不为0)表示双曲线的条件:
均不为0)表示双曲线的条件:
方程变形: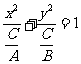 ,考察二次项系数的正负,若
,考察二次项系数的正负,若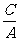 与
与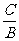 异号,表示双曲线;
异号,表示双曲线;
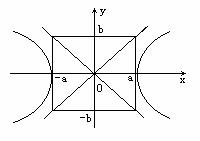 若
若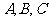 同号且
同号且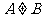 ,则表示椭圆;若
,则表示椭圆;若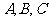 同号且
同号且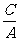 =
=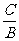 ,则表示圆.
,则表示圆.
1.双曲线定义:在平面内,到两个定点F1、F2的距离的差的绝对值等于常数(小于|F1F2|) 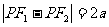 (
(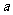 为常数
为常数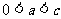 )的点的轨迹叫做双曲线.
)的点的轨迹叫做双曲线.
⑴若2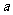 <
<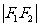 ,则动点P的轨迹是双曲线.
,则动点P的轨迹是双曲线.
⑵若2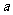 =
=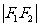 ,则动点P的轨迹是以F1,F2为端点的两条射线(在直线F1,F2上).
,则动点P的轨迹是以F1,F2为端点的两条射线(在直线F1,F2上).
⑶若2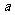 >
>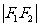 ,则动点P无轨迹.
,则动点P无轨迹.
22.(本小题满分12分)
已知过点A(1,1)且斜率为-m(m>0)的直线l与x轴、y轴分别交于P、Q,过P、Q作直线2x+y=0的垂线,垂足为R、S,求四边形PRSQ面积的最小值。

衡水中学2009-20010学年度小学期第二次调研考试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com