
题目列表(包括答案和解析)
20、(本小题满分12分)
解:由f(x)为二次函数知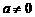
令f(x)=0解得其两根为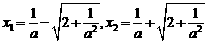
由此可知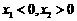 2分
2分
(i)当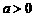 时,
时,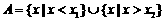
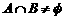 的充要条件是
的充要条件是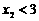 ,即
,即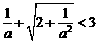 解得
解得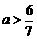 6分
6分
(ii)当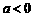 时,
时,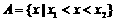
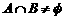 的充要条件是
的充要条件是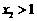 ,即
,即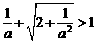 解得
解得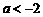 10分
10分
综上,使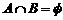 成立的a的取值范围为
成立的a的取值范围为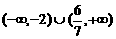 12分
12分
19、(本小题满分12分)

(Ⅰ)证明:
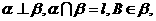 点B在
点B在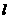 上的射影为
上的射影为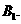
 BB1⊥
BB1⊥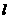 , 又BB1
, 又BB1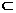
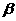
 BB1⊥α,又BB1
BB1⊥α,又BB1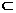 平面ABB1
平面ABB1
 平面ABB
平面ABB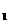
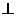 平面
平面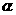 .
4分
.
4分
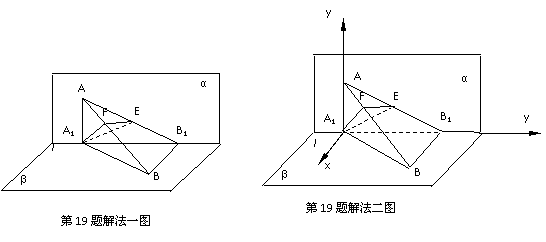
(Ⅱ) 解法一: ∵BB1⊥α, ∴平面ABB1⊥α.在平面α内过A1作A1E⊥AB1交AB1于E,则A1E⊥平面AB1B.过E作EF⊥AB交AB于F,连接A1F,则由三垂线定理得A1F⊥AB, ∴∠A1FE就是所求二面角的平面角.
在Rt△ABB1中,∠BAB1=45°,∴AB1=B1B=. ∴Rt△AA1B中,A1B== = . 由AA1·A1B=A1F·AB得 A1F== = , ∴在Rt△A1EF中,sin∠A1FE = = , ∴二面角A1-AB-B1的大小为arcsin. 12分
解法二: 如图,建立坐标系, 则A1(0,0,0),A(0,0,1),B1(0,1,0),B(,1,0).在AB上取一点F(x,y,z),则存在t∈R,使得=t , 即(x,y,z-1)=t(,1,-1), ∴点F的坐标为(t, t,1-t).要使⊥,须·=0, 即(t, t,1-t) ·(,1,-1)=0, 2t+t-(1-t)=0,解得t= , ∴点F的坐标为(,-, ), ∴=(,, ). 设E为AB1的中点,则点E的坐标为(0,, ). ∴=(,-,).
又·=(,-,)·(,1,-1)= - - =0, ∴⊥,
∴∠A1FE为所求二面角的平面角.又cos∠A1FE= = = = = ,
∴二面角A1-AB-B1的大小为arccos 12分
 高.考.资.源.网
高.考.资.源.网
18、(本小题满分12分)
解:(I) 所求概率P=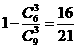 .
4分
.
4分
(II) 由题设知,顾客每次抽奖时,获奖概率都是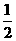 .设商场将奖金数额定为x元,
.设商场将奖金数额定为x元,
某顾客在3次抽奖中所获得的奖金总额为ξ元,则ξ的分布列为:

所以Eξ=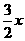 ,由题意得:
,由题意得: 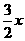 ≤180,∴x≤120.
≤180,∴x≤120.
即商场将奖金数额最高定为120元时,才能使促销方案对商场有利. 12分
高.考.资.源.网
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
D |
A |
B |
D |
C |
C |
B |
C |
A |
A |
C |
B |
高.考.资.源.网
22、(本小题满分12分)高.考.资.源.网
已知点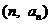
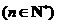 在函数
在函数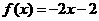 的图象上,数列
的图象上,数列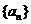 的前
的前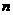 项和为
项和为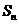 ,数列
,数列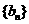 的前
的前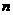 项和为
项和为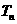 ,且
,且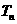 是
是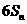 与
与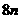 的等差中项。高.考.资.源.网
的等差中项。高.考.资.源.网
(Ⅰ)求数列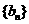 的通项公式;高.考.资.源.网
的通项公式;高.考.资.源.网
(Ⅱ)设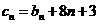 ,数列
,数列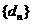 满足
满足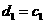 ,
,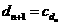
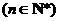 ,求数列
,求数列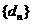 的前
的前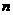 项和
项和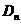 .高.考.资.源.网
.高.考.资.源.网
昆一中2008---2009学年下学期期末考高.考.资.源.网
21、(本小题满分12分)高.考.资.源.网
在平面直角坐标系 中,经过点
中,经过点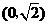 且斜率为
且斜率为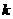 的直线
的直线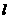 与椭圆
与椭圆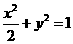 有两个不同的交点
有两个不同的交点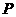 和
和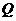 .高.考.资.源.网
.高.考.资.源.网
(I)求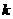 的取值范围;高.考.资.源.网
的取值范围;高.考.资.源.网
(II)设椭圆与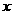 轴正半轴、
轴正半轴、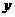 轴正半轴的交点分别为
轴正半轴的交点分别为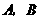 ,是否存在常数
,是否存在常数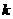 ,使得向量
,使得向量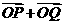 与
与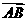 共线?如果存在,求
共线?如果存在,求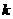 值;如果不存在,请说明理由。高.考.资.源.网
值;如果不存在,请说明理由。高.考.资.源.网
高.考.资.源.网
高.考.资.源.网
20、(本小题满分12分)高.考.资.源.网
已知二次函数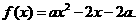 (
(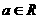 ),若
),若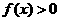 的解集为A,
的解集为A,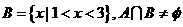 ,求实数
,求实数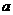 的取值范围。高.考.资.源.网
的取值范围。高.考.资.源.网
高.考.资.源.网
高.考.资.源.网
高.考.资.源.网
19、(本小题满分12分)高.考.资.源.网
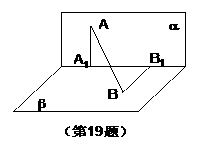 如图,
如图,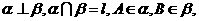 点A在直线
点A在直线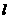 上的射影为
上的射影为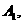 点B在
点B在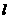 上的射影为
上的射影为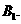 已知
已知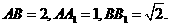 高.考.资.源.网
高.考.资.源.网
(I)求证:平面ABB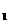
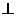 平面
平面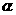 ;高.考.资.源.网
;高.考.资.源.网
(II)求二面角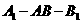 的大小高.考.资.源.网
的大小高.考.资.源.网
(用反三角表示)。高.考.资.源.网
18、(本小题满分12分)高.考.资.源.网
某家电商场准备在“五一”期间举行促销活动.根据市场调查,该商场决定:从4种冰箱、3种空调、2种彩电共9种商品中选出3种进行促销活动。高.考.资.源.网
(Ⅰ) 试求选出的3种商品中有空调的概率;高.考.资.源.网
(Ⅱ) 商场对选出的促销商品进行有奖销售,其方案是:在每件商品现价的基础上提高180元,顾客每购一件促销商品均有3次抽奖机会,每次中奖均可获得奖金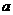 元。假设顾客每次抽奖时获奖与否的概率相等。试问商场将奖金数额
元。假设顾客每次抽奖时获奖与否的概率相等。试问商场将奖金数额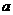 最高定为多少元时,才能使促销方案对商场有利?高.考.资.源.网
最高定为多少元时,才能使促销方案对商场有利?高.考.资.源.网
高.考.资.源.网
高.考.资.源.网
高.考.资.源.网
17、(本小题满分10分)高.考.资.源.网
已知向量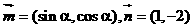 , 且
, 且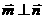 .高.考.资.源.网
.高.考.资.源.网
(Ⅰ) 求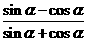 的值;高.考.资.源.网
的值;高.考.资.源.网
(Ⅱ) 求函数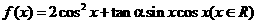 的最小值.高.考.资.源.网
的最小值.高.考.资.源.网
高.考.资.源.网
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com