
题目列表(包括答案和解析)
1.给出下列4个命题:①若sin2A=sin2B,则△ABC是等腰三角形;②若sinA=cosB,则△ABC是直角三角形;③若cosAcosBcosC<0,则△ABC是钝角三角形;④若cos(A-B)cos(B-C)cos(C-A)=1,则△ABC是等边三角形. 其中正确的命题是 ( )
(A)①③ (B)③④ (C)①④ (D)②③
重点:①能充分应用三角形的性质及有关的三角函数公式证明三角形的边角关系式.②能合理地选用正弦定理余弦定理结合三角形的性质解斜三角形.③能解决与三角形有关的实际问题.
难点:①根据已知条件判定解的情形,并正确求解.②将实际问题转化为解斜三角形.
在高考试题中,有关解三角形的内容并不多,出现的有关试题大多属于容易题,最高到中档题,主要考察正弦定理余弦定理及利用三角公式进行恒等变形的技能及运算能力,以化简、求值或判断三角形的形状为主,考察有关定理的应用、三角恒等变换的能力及转化的数学思想.
22. (12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
(12分)已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且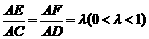
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD?
21.(12分)已知椭圆的中心在原点,焦点在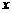 轴上,离心率为
轴上,离心率为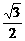 ,若
,若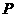 是椭圆上的动点,且
是椭圆上的动点,且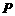 到焦点距离的最大值为
到焦点距离的最大值为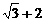 ,设定点A(1,
,设定点A(1,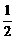 ),
),
(1)求该椭圆的标准方程;
(2)求线段 中点
中点 的轨迹方程。
的轨迹方程。
20.(12分)已知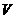 是平面
是平面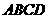 外一点,平面
外一点,平面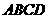 是边长为
是边长为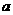 的正方形,侧面
的正方形,侧面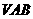 是等边三角形,且平面
是等边三角形,且平面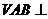 平面
平面
(1)求 与平面
与平面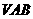 所成的角;
所成的角;
 (2)求二面角
(2)求二面角 的正切值。
的正切值。
19.(12分) 已知双曲线中心在原点,且一个焦点为F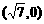 ,直线
,直线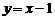 与其相交于M,N两点,MN中点的横坐标为
与其相交于M,N两点,MN中点的横坐标为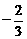 ,求此双曲线的方程。
,求此双曲线的方程。
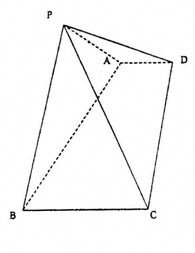
18. (12分)如图,已知四棱锥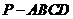 的底面为直角梯形,AD∥BC,∠BCD=90°,PA=PB,PC=PD
的底面为直角梯形,AD∥BC,∠BCD=90°,PA=PB,PC=PD
(1)证明:平面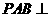 平面ABCD;
平面ABCD;
(2)如果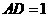
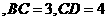 ,且侧面
,且侧面 的面积为8,
的面积为8,
 求四棱锥
求四棱锥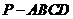 的体积。
的体积。
17.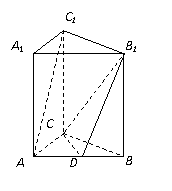 (10分)如图,三棱柱
(10分)如图,三棱柱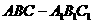 的侧棱与底面垂直,
的侧棱与底面垂直,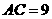 ,
,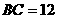 ,
, ,
,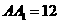 ,
,
点D是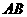 的中点.
的中点.
⑴求证: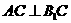 ;
;
⑵求证: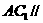 平面
平面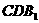 .
.
16.下列命题中:
①若 为两个命题,则“
为两个命题,则“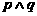 为真”是“
为真”是“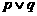 为真”的必要不充分条件;
为真”的必要不充分条件;
②若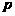 为:
为: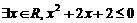 ,则
,则 为:
为: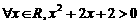 ;
;
③ ;
;
④设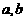 是空间两条垂直的直线,且
是空间两条垂直的直线,且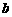 ∥平面
∥平面 ,则在“
,则在“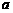 ∥
∥ ”、“
”、“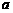
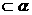 ”、“
”、“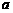 与
与 相交”这三种情况中,能够出现的情况有3个.
相交”这三种情况中,能够出现的情况有3个.
所有正确的命题的序号是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com