
题目列表(包括答案和解析)
1. 复数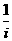 等于
( )
等于
( )
A.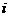 B.
B.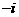 C.1 D.-1
C.1 D.-1
(17)(本题满分8分)
解:
从5个球中任意摸出2个共有10种不同的结果.
 分
分
记从5个球中任取2个,其中恰有1个红球为事件 ,恰有2个红球为事件
,恰有2个红球为事件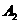 ,恰有1个红球或恰有2个红球为事件
,恰有1个红球或恰有2个红球为事件 ,
,
 分
分
则事件 发生的概率,即为“所得分数不小于8分”的概率
发生的概率,即为“所得分数不小于8分”的概率
而,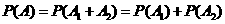
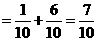
 分
分
(或者,设所求事件的对立事件为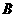 ,则
,则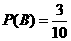 ,
,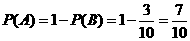 )
)
故“所得分数不小于8分”的概率为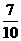
 分
分
(18)(本题满分8分)
解:由题意,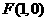 ,直线
,直线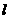 的方程为
的方程为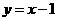
 分
分
由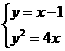 得,
得,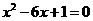 ,
,
 分
分
设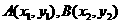 ,圆心
,圆心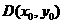 ,半径为R
,半径为R
则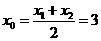 ,
,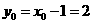 .
.
 分
分
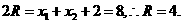
所以,所求圆的标准方程为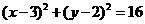 .
.
 分
分
(19)(本题满分10分)
解:(Ⅰ)设双曲线方程为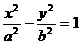 (
(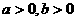 ),半焦距为
),半焦距为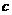
依题意得 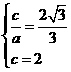 解得
解得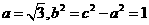
 分
分
 所求双曲线C的方程为
所求双曲线C的方程为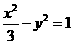
 分
分
(Ⅱ)依题意有: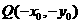 ,
,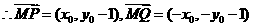
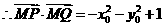 ,又
,又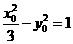
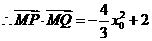 ,
,
 分
分
由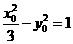 可得,
可得,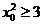
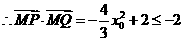
故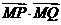 的取值范围是
的取值范围是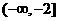
 分
分
(20)(本题满分10分)
解:法一:(Ⅰ)证明: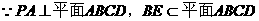 ,
,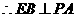 .
.
又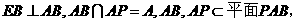
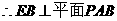 ,
,
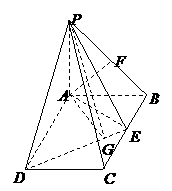 又
又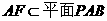 ,∴
,∴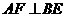
 分
分
又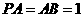 ,点
,点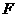 是
是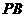 的中点,
的中点,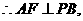
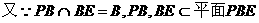 ,
,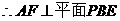 .
.
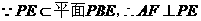 .
.  分
分
(Ⅱ)过 作
作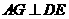 于
于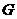 ,连
,连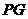 ,又∵
,又∵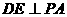 ,
,
则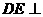 平面
平面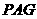 ,
,
则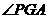 是二面角
是二面角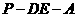 的平面角,
的平面角,
∴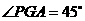
∵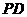 与平面
与平面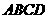 所成角是
所成角是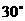 ,∴
,∴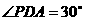 ,
,
∴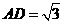 ,
,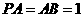 .
.
 分
分
∴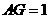 ,
,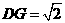 ,设
,设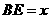 ,则
,则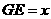 ,
,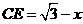 ,
,
 在
在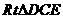 中,
中,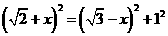 ,
,
得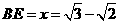 .故
.故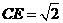 。
。  分
分
法二:(Ⅰ)建立图示空间直角坐标系,则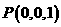 ,
,
∵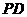 与平面
与平面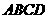 所成角是
所成角是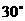 ,∴
,∴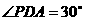 ,
,
∴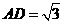 ,
,
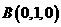 ,
,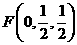 ,
,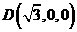 .
.  分
分
设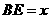 ,则
,则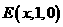
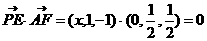
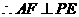 .
.
 分
分
(Ⅱ)设平面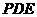 的法向量为
的法向量为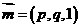 ,由
,由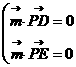 ,得:
,得: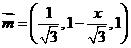 ,
,
 分
分
而平面 的法向量为
的法向量为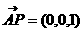 ,∵二面角
,∵二面角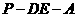 的大小是
的大小是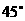 ,所以
,所以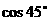 =
=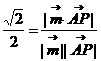 ,∴
,∴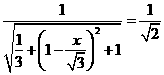 ,
,  分
分
得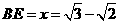 或
或 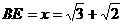 (舍).
(舍).
∴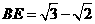 , 故
, 故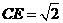 。
。  分
分
(21)(本题满分10分)
解:(Ⅰ)依题意得,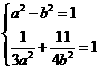 解得,
解得,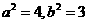
∴椭圆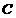 的方程是
的方程是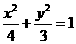
 分
分
(Ⅱ)法一:若直线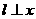 轴,则直线
轴,则直线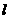 的方程为
的方程为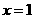 ,易知
,易知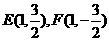
 的面积
的面积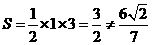 ,所以直线
,所以直线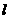 的率存在且不为0,可设
的率存在且不为0,可设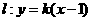 ,
,
由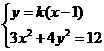 得,
得,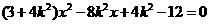 ,设
,设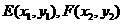
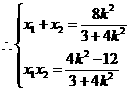 ,
,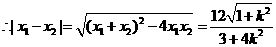
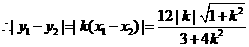
 分
分
 的面积为
的面积为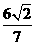 ,
,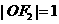 ,
,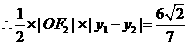 ,
,
解得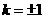 ,所以直线
,所以直线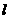 的方程为:
的方程为: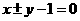
 分
分
法二:若直线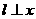 轴,则直线
轴,则直线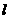 的方程为
的方程为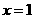 ,易知
,易知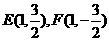
 的面积
的面积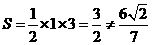 ,所以直线
,所以直线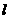 的率存在且不为0,可设
的率存在且不为0,可设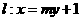 ,
,
由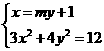 得,
得,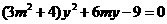 ,设
,设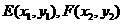
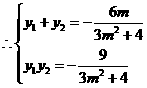 ,
,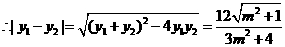
 的面积为
的面积为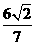 ,
,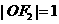 ,
,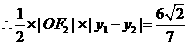 ,
,
解得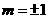 ,所以直线
,所以直线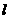 的方程为:
的方程为: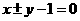
(22)(本题满分10分)
解:(Ⅰ)函数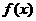 定义域为
定义域为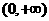
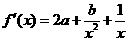
 分
分
依题意得,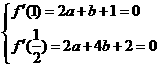 ,解得,
,解得,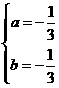
故所求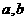 的值为
的值为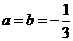
 分
分
(Ⅱ)在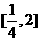 上存在
上存在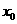 ,使不等式
,使不等式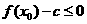 成立,只需
成立,只需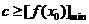
由(Ⅰ)知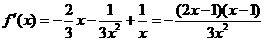
当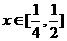 时,
时,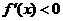 ,故函数
,故函数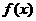 在
在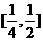 上单调递减,
上单调递减,
当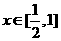 时,
时,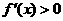 ,故函数
,故函数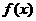 在
在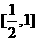 上单调递增,
上单调递增,
当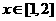 时,
时,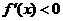 ,故函数
,故函数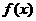 在
在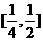 上单调递减
上单调递减  分
分
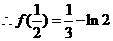 是
是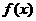 在
在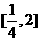 上的极小值,且函数
上的极小值,且函数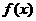 的最小值必是
的最小值必是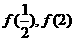 两者中较小的
两者中较小的
 分
分
而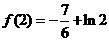 ,
,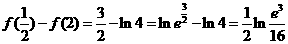
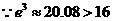 ,
,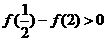
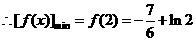
 分
分
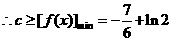
所以,实数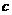 的最小值为
的最小值为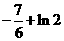 .
.
 分
分
(13)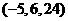 ; (14)
; (14)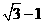 ; (15)
; (15)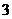 ; (16)4
; (16)4
AABBD,CCCBC,BA
第Ⅱ卷(非选择题,共72分)
(17)(本题满分8分)
袋中有2个红球,3个白球,摸出一个红球得5分,摸出一个白球得3分,现从中任意摸出2个球,求事件“所得分数不小于8分”的概率.
(18)(本题满分8分)
已知抛物线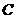 :
: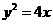 的焦点为
的焦点为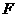 ,直线
,直线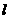 过点
过点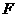 且其倾斜角为
且其倾斜角为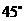 ,设直线
,设直线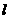 与曲线
与曲线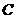 相交于
相交于 、
、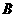 两点,求以线段
两点,求以线段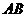 为直径的圆的标准方程.
为直径的圆的标准方程.
(19)(本题满分10分)
已知双曲线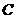 的中心在坐标原点
的中心在坐标原点 ,对称轴为坐标轴,点
,对称轴为坐标轴,点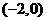 是它的一个焦点,并且离心率为
是它的一个焦点,并且离心率为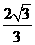 .
.
(Ⅰ)求双曲线C的方程;
(Ⅱ)已知点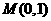 ,设
,设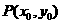 是双曲线
是双曲线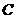 上的点,
上的点,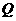 是点
是点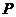 关于原点的对称点,
关于原点的对称点,
求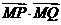 的取值范围.
的取值范围.
(20)(本题满分10分)
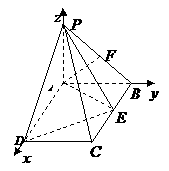
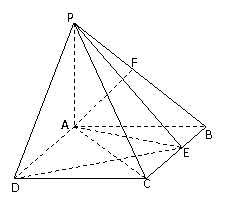 如图,
如图,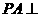 平面
平面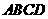 ,四边形
,四边形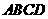 是矩形,
是矩形,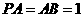 ,
,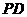 与平面
与平面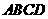 所成角是
所成角是 ,点
,点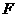 是
是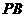 的中点,点
的中点,点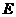 在矩形
在矩形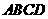 的边
的边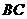 上移动.
上移动.
(Ⅰ)证明:无论点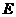 在边
在边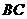 的何处,都有
的何处,都有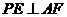 ;
;
(Ⅱ)当 等于何值时,二面角
等于何值时,二面角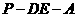 的大小为
的大小为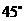 .
.
(21)(本题满分10分)
已知椭圆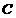 :
: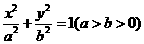 的两个焦点为
的两个焦点为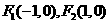 ,点
,点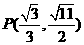 在椭圆
在椭圆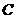 上.
上.
(Ⅰ)求椭圆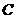 的方程;
的方程;
(Ⅱ)记 为坐标原点,过
为坐标原点,过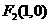 的直线
的直线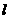 与椭圆
与椭圆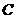 相交于
相交于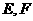 两点,若
两点,若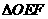 的面积为
的面积为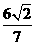 ,求直线
,求直线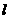 的方程.
的方程.
(22)(本题满分10分)
已知函数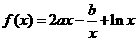 在
在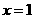 和
和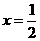 处取得极值.
处取得极值.
(Ⅰ)求实数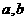 的值;
的值;
(Ⅱ)若函数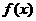 在区间
在区间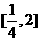 上存在
上存在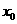 ,使得不等式
,使得不等式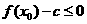 成立,求实数
成立,求实数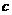 的最小值.(参考数据
的最小值.(参考数据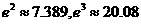 )
)
东北师大附中2009-2010学年度上学期
高二年级期末考试数学(理科)评分标准
第Ⅰ卷(选择题,共48分)
(13)已知点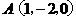 和向量
和向量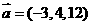 ,若
,若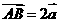 ,则点
,则点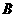 的坐标为
.
的坐标为
.
(14)设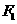 、
、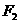 是椭圆
是椭圆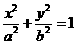
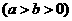 的两个焦点,以
的两个焦点,以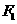 为圆心,且过椭圆中心的圆与椭圆的一个交点为
为圆心,且过椭圆中心的圆与椭圆的一个交点为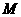 ,若直线
,若直线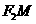 与圆
与圆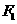 相切,则该椭圆的离心率是
.
相切,则该椭圆的离心率是
.
(15)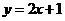 与曲线
与曲线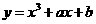 相切于点
相切于点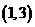 ,则
,则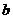 的值为
.
的值为
.
(16)已知点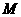 为抛物线
为抛物线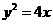 上一点,若点
上一点,若点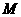 到直线
到直线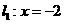 的距离为
的距离为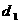 ,点
,点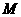 到直线
到直线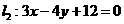 的距离为
的距离为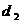 ,则
,则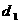 +
+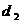 的最小值为
.
的最小值为
.
(1)命题“若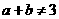 ,则
,则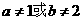 ”的逆否命题为
”的逆否命题为
(A)若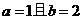 ,则
,则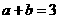 (B)若
(B)若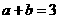 ,则
,则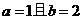
(C)若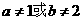 ,则
,则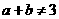 (D)若
(D)若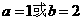 ,则
,则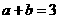
(2)若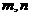 是实数,条件甲:
是实数,条件甲: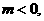 且
且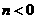 ;条件乙:方程
;条件乙:方程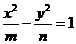 表示双曲线,则甲是乙的
表示双曲线,则甲是乙的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不是充分条件也不是必要条件
(3)在同一坐标系中,方程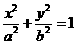 与
与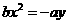
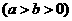 表示的曲线大致是
表示的曲线大致是

(A) (B) (C) (D)
(4)抛物线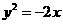 的焦点到准线的距离为
的焦点到准线的距离为
(A)2
(B)1
(C)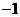 (D)
(D)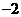
(5)某流程如右图所示,现输入如下四个函数,则可以输出的函数是

(A)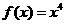
(B)
(C)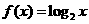
(D)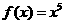
(6)函数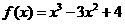 的单调递减区间为
的单调递减区间为
(A)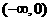 (B)
(B)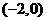 (C)
(C)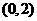 (D)
(D)
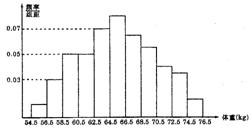 (7)为了了解长春市朝阳区高中学生的身体发育情况,有关部门抽查了该地区100名年龄为17-18岁的男生体重(
(7)为了了解长春市朝阳区高中学生的身体发育情况,有关部门抽查了该地区100名年龄为17-18岁的男生体重(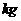 ),得到如下频率分布直方图,则这
),得到如下频率分布直方图,则这 名学生中,体重在
名学生中,体重在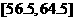 的学生人数是
的学生人数是
(A)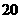 (B)
(B)
(C)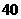 (D)
(D)
(8)设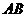 为过抛物线
为过抛物线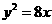 的焦点的弦,若
的焦点的弦,若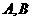 两点的坐标分别为
两点的坐标分别为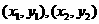 ,
,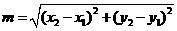 ,则实数
,则实数 的最小值为
的最小值为
(A)2 (B)4 (C)8 (D)16
(9)函数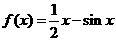 在
在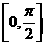 上的最小值是
上的最小值是
(A)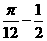 (B)
(B) 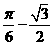 (C)
(C) (D)
(D) 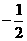
(10)以下四图,都是同一坐标系中三次函数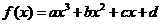
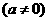 及其导函数的图像,其中一定不正确的序号是
及其导函数的图像,其中一定不正确的序号是
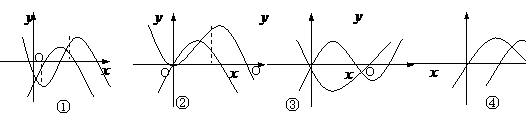
(A)①、② (B)①、③ (C)③、④ (D)①、④
(11)已知两定点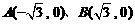 ,直线
,直线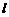 过点
过点 且与直线
且与直线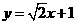 平行,则
平行,则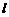 上满足
上满足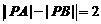 的点
的点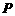 的个数为
的个数为
(A)0 (B) 1 (C)2 (D) 无法确定
(12)过椭圆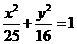 内一点(0,2)的弦的中点的轨迹方程为
内一点(0,2)的弦的中点的轨迹方程为
(A)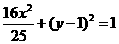 (B)
(B)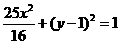
(C)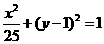 (D)
(D)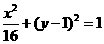
第Ⅱ卷(非选择题,共72分)
22.(本小题满分12分)
已知定点C(-1,0)及椭圆x2+3y2=5,过点C的动直线与椭圆相交于A、B两点.
(Ⅰ)若线段AB中点的横坐标是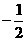 ,求直线AB的方程;
,求直线AB的方程;
(Ⅱ)在x轴上是否存在点M,使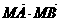 恒为常数?若存在,求出点M的坐标和常数的值;若不存在,请说明理由.
恒为常数?若存在,求出点M的坐标和常数的值;若不存在,请说明理由.
21.(本小题满分12分)
已知双曲线 (a>0,b>0)的离心率
(a>0,b>0)的离心率 ,过点A(0,―b)和B(a,0)的直线与原点间的距离是
,过点A(0,―b)和B(a,0)的直线与原点间的距离是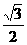 .
.
(Ⅰ)求双曲线的方程;
(Ⅱ)若直线y=kx+5 (k≠0)与双曲线交于不同的两点C、D,且两点都在以A为圆心的同一个圆上,求k的值.
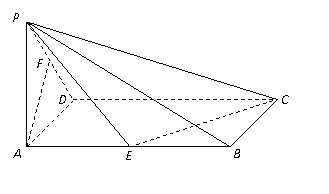
20.(本小题满分12分)
已知在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点.
(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求PC与平面ABCD所成角的正弦值;
(Ⅲ)求二面角P-EC-D的余弦值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com