
题目列表(包括答案和解析)
7.如果袋中有六个红球,四个白球,从中任取一个球,记住颜色后放回,连续摸取4次,设X为取得红球的次数,则X的期望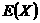 =
=
A. B.
B.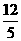 C.
C.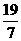 D.
D.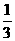
6.设随机变量X的分布列如下:
其中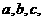 成等差数列,若
成等差数列,若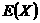 =
=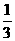 ,则
,则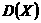 的值是
的值是
A. 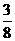 B.
B.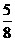 C.
C.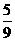 D.
D.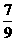
5.在一次试验中,当变量x的取值分别为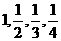 时,变量y的值依次为2,3,4,5,则y与
时,变量y的值依次为2,3,4,5,则y与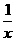 之间的回归曲线方程是
之间的回归曲线方程是
A.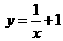 B.
B.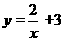 C.
C.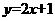 D.
D.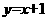
|
X |
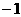 |
0 |
1 |
|
P |
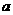 |
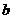 |
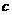 |
4.一个质点位于坐标原点O处,此质点每秒钟只向左或向右移动一个单位,向左和向右移动的机会均等,则3秒后此质点位于(1,0)处的概率为
A.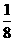 B.
B.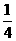 C.
C.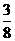 D.
D.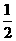
3.设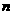 为自然数,则
为自然数,则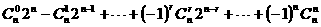 等于
等于
A.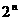 B.0
C.
B.0
C.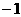 D.
D.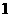
2.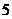 名运动员进行
名运动员进行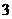 项体育运动比赛,每项只设有冠军和亚军各一名,那么各项冠军获得者的不同情况的种数为
项体育运动比赛,每项只设有冠军和亚军各一名,那么各项冠军获得者的不同情况的种数为
A.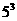 B.
B.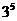 C.
C.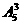 D.
D.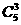
1.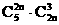 =
=
A.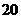 B.
B. 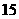 C.
C. 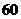 D.
D.
(17)(本题满分14分)
<ppt><1>已<\ppt>知p:|1-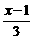 |≤2,q:x2-2x+1-m2≤0(m>0),若
|≤2,q:x2-2x+1-m2≤0(m>0),若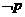 是
是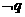 的必要而不充分条件,
求实数m的取值范围.
的必要而不充分条件,
求实数m的取值范围.
(18)(本题满分14分)
如图,在四棱锥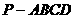 中,底面
中,底面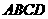 是正方形,侧棱
是正方形,侧棱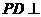 底面
底面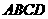 ,
,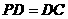 ,
,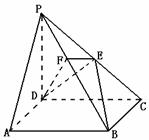
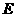 是
是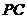 的中点,作
的中点,作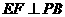 交
交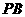 于点
于点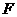 .
.
(Ⅰ)证明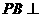 平面
平面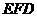 ;
;
(Ⅱ)求二面角 的大小.
的大小.
(19) (本题满分14分)
在ΔABC中,角A、B、C所对的边 分别为a、b、c,且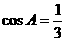 。
。
(Ⅰ)求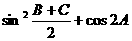 的值;
的值;
(Ⅱ)若 ,求bc的最大值。
,求bc的最大值。
(20)(本题满分14分)
过点(1,0)的直线l与中心在原点,焦点在x轴上且离心率为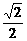 的椭圆C相交于A、B两点,直线y=
的椭圆C相交于A、B两点,直线y=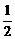 x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
x过线段AB的中点,同时椭圆C上存在一点与右焦点关于直线l对称,试求直线l与椭圆C的方程.
(21)(本题满分14分)
已知数列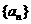 的各项均为正数,
的各项均为正数,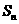 为其前
为其前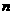 项和,且对任意的
项和,且对任意的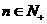 ,有
,有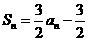 .
.
(Ⅰ)求数列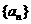 的通项公式;
的通项公式;
(Ⅱ)设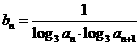 ,求数列
,求数列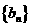 的前
的前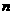 项和
项和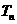 .
.

|

|
 版权所有:()
版权所有:()
版权所有:()
版权所有:()
辽宁省锦州市09-10学年高二上学期期末考试
(13)在△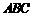 中,已知
中,已知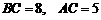 ,三角形面积为12,则
,三角形面积为12,则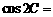 .
.
(14)在等差数列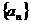 中,若
中,若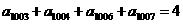 ,则该数列的前2009项的和是
.
,则该数列的前2009项的和是
.
(15)某高校录取新生对语文、数学、英语的高考分数的要求是:1语文不低于70分;2数学应高于80分;3三科成绩之和不少于230分。若张三被录取到该校,则该同学的语、数、英成绩x、y、z应满足的约束条件是_____________________.
(16)设斜率为2的直线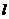 过抛物线
过抛物线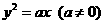 的焦点F,且和
的焦点F,且和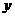 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为_____________________.
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为_____________________.
(1)下列曲线中离心率为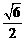 的是( )
的是( )
(A)
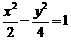 (B)
(B) 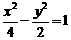 (C)
(C) 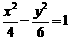 (D)
(D) 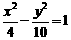
(2)在△ABC中,若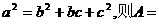 ( )
( )
A. 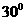 B.
B. C.
C.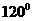 D.
D.
(3)“a=1”是函数y=cos2ax-sin2ax的最小正周期为“π”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既非充分条件也不是必要条件
(4)已知向量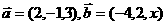 ,使
,使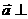
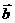 成立的x与使
成立的x与使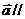
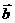 成立的x分别为( )
成立的x分别为( )
A.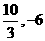 B.-
B.-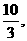 6 C.-6,
6 C.-6,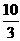 D.6,-
D.6,-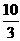
(5)命题“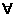
 ,
,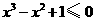 ”的否定是 ( )
”的否定是 ( )
A.不存在 ,
,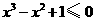 B.存在
B.存在 ,
,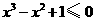
C.存在 ,
,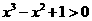 D.对任意的
D.对任意的 ,
,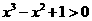
(6)设A1、A2是椭圆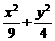 =1的长轴两个端点,P1、P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
=1的长轴两个端点,P1、P2是垂直于A1A2的弦的端点,则直线A1P1与A2P2交点的轨迹方程为( )
A.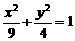 B.
B.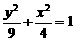
C.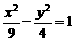 D.
D.
(7)在等比数列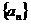 中,已知
中,已知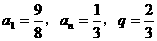 ,则n为 ( )
,则n为 ( )
A.2 B.3 C.4 D.5
(8)下列结论中,错用基本不等式做依据的是 ( )
A.a,b均为负数,则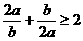 B.
B.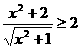
C.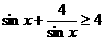 D.
D.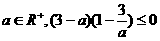
(9)若A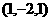 ,B
,B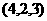 ,C
,C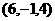 ,则△ABC的形状是 ( )
,则△ABC的形状是 ( )
A.不等边锐角三角形 B.直角三角形
C.钝角三角形 D.等边三角形
(10)已知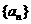 为等差数列,且
为等差数列,且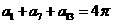 ,则
,则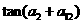 的值为
( B )
的值为
( B )
A.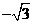 B.
B.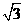 C.
C.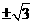 D.
D.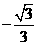
(11)在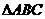 中,
中,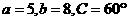 ,则
,则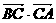 的值为
(
)
的值为
(
)
A.10 B. 20 C.-10 D.-20
(12)已知y=f(x)是R上的减函数,且y=f(x)的图象经过点A(0,1)和点B(3,-1),则不等
式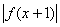 <1的解集为( )
A.(-1,2) B.(0,3) C.(-∞,-2) D.(-∞,3)
<1的解集为( )
A.(-1,2) B.(0,3) C.(-∞,-2) D.(-∞,3)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com