
题目列表(包括答案和解析)
6. 设函数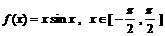 ,若
,若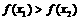 ,则下列不等式必定成立的是(
)
,则下列不等式必定成立的是(
)
A.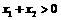 B.
B.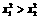 C.
C.
 D.
D. 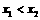
5.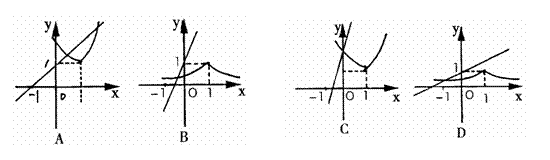 已知函数
已知函数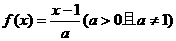 ,在同一直角坐标系中,
,在同一直角坐标系中,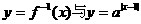 的图象可能是( )
的图象可能是( )
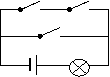
4. 已知数列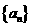 的通项公式
的通项公式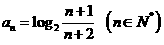 ,设其前n项和为Sn,则使
,设其前n项和为Sn,则使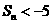 成立的自然数n
( )A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
成立的自然数n
( )A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
3. 设函数f(x)是定义在R上的以3为周期的奇函数,若f(1)>1,f(2)=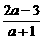 ,则( )
,则( )
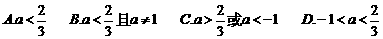
2. 设集合M={-1,1,0},N={1,2,3,4,5}, 映射f: M→N,使对任意的x∈M,都有x+f(x)是奇数,这样的映射f的个数为( )
A.10 B.11 C.12 D.13
1. 已知i,j为互相垂直的单位向量,a = i – 2j,b = i + λj且a与b的夹角为锐角,则实数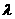 的取值范围是( )
的取值范围是( )
A.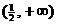 B.
B.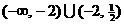 C.
C.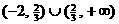 D.
D.
9.(94年全国理)设{an}是正数组成的数列,其前n项和为Sn,并且对所有自然数n,an与2的等差中项等于Sn与2的等比中项.
(1)写出数列{an}的前三项; (2)求数列{an}的通项公式(写出推证过程);
(3)令bn=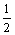
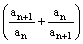 (n∈N),求:b1+b2+…+bn-n.
(n∈N),求:b1+b2+…+bn-n.
8.(2002年春招试题)已知点的序列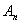 (
(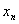 ,0),
,0),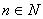 ,其中
,其中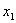 =0,
=0,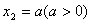 ,A3是线钱A1A2的中点,A4是线段A2A3的中点,…,An是线段
,A3是线钱A1A2的中点,A4是线段A2A3的中点,…,An是线段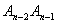 的中点,…。
的中点,…。
(I)写出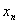 与
与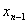 、
、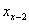 之间的关系式(
之间的关系式(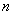 ≥3)
≥3)
(II)设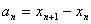 ,计算
,计算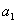 ,
,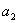 ,
,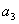 ,由此推测数列{
,由此推测数列{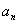 }的通项公式,并加以证明。
}的通项公式,并加以证明。
7.某县位于沙漠地带,人与自然长期进行着顽强的斗争,到2001年底全县的绿化率已达30%。从2002年开始,每年将出现这样的局面,即原有沙漠面积的16%将被绿化,与此同时,由于各种原因,原有绿化面积的4%又被沙化。
(1)设全县面积为1,2001年底绿化面积为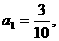 经过
经过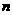 年绿化总面积为
年绿化总面积为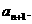
求证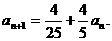
(2)至少需要多少年(年取整数,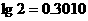 )的努力,才能使全县的绿化率达到60%?
)的努力,才能使全县的绿化率达到60%?
6.数列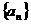 的前
的前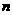 项和
项和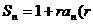 为不等于0,1的常数),求其通项公式
为不等于0,1的常数),求其通项公式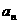
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com