
题目列表(包括答案和解析)
6.x、y∈R,x2+y2=1,那么(1-xy)(1+xy)有
A.最小值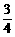 和最大值1 B.最小值
和最大值1 B.最小值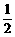 和最大值1
和最大值1
C.最小值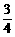 无最大值 D.最小值
无最大值 D.最小值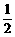 无最大值
无最大值
解析:令x=cosθ,y=sinθ,
则(1-xy)(1+xy)=1-x2y2=1-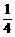 sin22θ.
sin22θ.
∵0≤sin22θ≤1,∴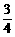 ≤1-
≤1-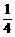 sin22θ≤1.
sin22θ≤1.
答案:A
5.已知函数y=lg(x2-2kx+k)的值域为R,则k的取值范围是
A.0<k<1 B.0≤k≤1
C.k≤0或k≥1 D.k=0或k≥1
解析:Δ≥0 k≥1或k≤0.
k≥1或k≤0.
答案:C
4.已知方程x2+(m+2)x+m+5=0有两个正实根,则实数m的取值范围是
A.m<-2 B.m≤-4
C.m>-5 D.-5<m≤-4
解析: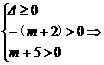 -5<m≤-4.
-5<m≤-4.
答案:D
3.不等式(x+1)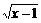 ≥0的解集是
≥0的解集是
A.{x|x>1} B.{x|x≥1}
C.{x|x≥1或x=-1} D.{x|x≥-1或x=1}
解析:∵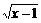 ≥0,∴x≥1.
≥0,∴x≥1.
又∵x+1=0,不等式成立.∴x=-1.选C.
答案:C
2.设x、y∈R,那么|x|<1且|y|<1是0<xy<1成立的____________条件.
A.充分不必要 B.必要不充分
C.充要 D.既不充分也不必要
解析:设x=-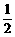 ,y=0,则xy=0.不能推出0<xy<1;
,y=0,则xy=0.不能推出0<xy<1;
设x=2,y=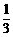 满足0<xy<1,不能推出|x|<1且|y|<1.
满足0<xy<1,不能推出|x|<1且|y|<1.
答案:D
1.已知集合M={x|-1<x<2},N={y|y=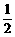 x2-1,x∈M},则M∩N为
x2-1,x∈M},则M∩N为
A.{a|-1≤a<2} B.{a|-1<a<2}
C.{a|-1<a<1} D.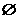
解析:y=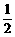 x2-1,x∈(-1,2).
x2-1,x∈(-1,2).
所以y∈[-1,1).
答案:C
20. (本小题满分14分)
(1) 依题意,可设直线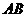 的方程为
的方程为 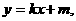 代入抛物线方程
代入抛物线方程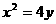 得
得
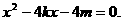 ①
①
设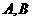 两点的坐标分别是
两点的坐标分别是 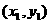 、
、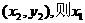 、
、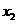 是方程①的两根.
是方程①的两根.
所以 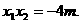 ---
2分
---
2分
由点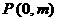 分有向线段
分有向线段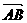 所成的比为
所成的比为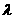 ,得
,得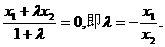
又点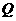 与点
与点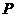 关于原点对称,故点
关于原点对称,故点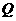 的坐标是
的坐标是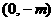 ,从而
,从而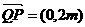 .--- 2分
.--- 2分
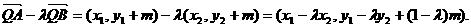 --- 2分
--- 2分
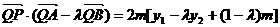
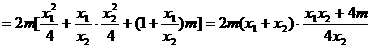
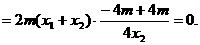 所以
所以
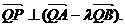 ---
2分
---
2分
(2) 由 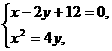 得点
得点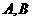 的坐标分别是(6,9)、(-4,4), --- 2分
的坐标分别是(6,9)、(-4,4), --- 2分
由 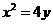 得
得 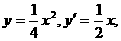
所以抛物线 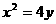 在点
在点 处切线的斜率为
处切线的斜率为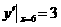 ,
--- 2分
,
--- 2分
设圆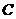 的圆心为
的圆心为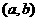 , 方程是
, 方程是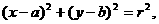
则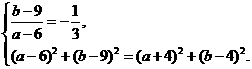 解得
解得 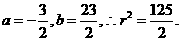
则圆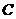 的方程是
的方程是 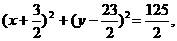 (或
(或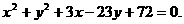 )
)
--- 2分
19.(本小题满分14分)
(1) 由奇函数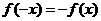 可得
可得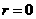 ,
--- 2分
,
--- 2分
x > 0时,由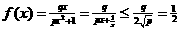 ① 以及
① 以及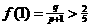 ②
--- 4分
②
--- 4分
可得到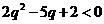 ,
, 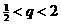 , 只有
, 只有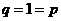 , ∴
, ∴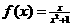 ; --- 2分
; --- 2分
(2) 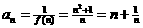 ,
--- 2分
,
--- 2分
则由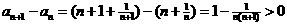 (
(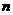 是正整数),
是正整数),
可得所求证结论. --- 4分
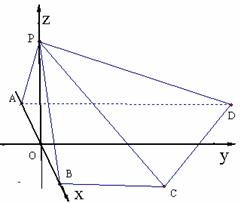
18. (本小题满分14分)
因为 中点
中点 为点
为点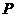 在平面ABCD内的射影, 所以
在平面ABCD内的射影, 所以 底面
底面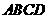 . 以
. 以 为坐标原点,
为坐标原点, 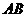 所在直线为
所在直线为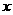 轴,
轴, 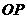 所在直线为
所在直线为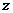 轴, 建立空间直角坐标系
轴, 建立空间直角坐标系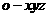 (如图).
(如图).
(1)设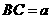 , OP = h则依题意得:
, OP = h则依题意得:
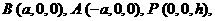
|
--- 4分 |
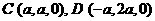 .
.
∴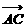 =
= 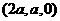 ,
, 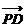 =
= 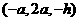 ,
,
于是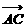 ·
·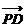 =
= 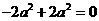 , ∴
, ∴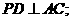
(2)由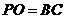 , 得h = a, 于是
, 得h = a, 于是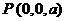 ,
,
|
--- 5分 |
∵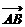 =
= 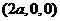 ,
, 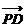 =
= 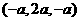 , ∴
, ∴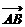 ·
·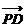 =
= 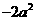 ,
,
cos<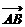 ,
,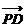 > =
> = 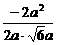 =
=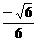 , ∴ 直线
, ∴ 直线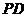 与
与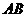 所成的角的余弦值为
所成的角的余弦值为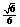 ;
;
(3)
设平面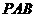 的法向量为m, 可得m = (0,1,0 ),
的法向量为m, 可得m = (0,1,0 ),
设平面 的法向量为n =
的法向量为n = 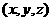 , 由
, 由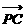 =
= 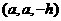 ,
, 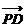 =
= 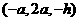 ,
,
∴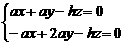 , 解得n = (1, 2 ,
, 解得n = (1, 2 ,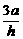 ), ∴ m•n = 2 ,
), ∴ m•n = 2 ,
cos< m, n > = 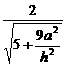 , ∵ 二面角为
, ∵ 二面角为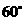 , ∴
, ∴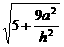 = 4,
= 4,
解得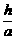 =
=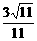 ,即
,即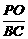 =
=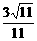 .
--- 5分
.
--- 5分
(以传统方法解答相应给分)
17.(本小题满分14分)
设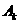 表示“第
表示“第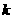 人命中目标”,
人命中目标”,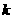 =1,2,3.
=1,2,3.
这里,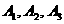 相互独立,且
相互独立,且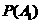 =0.7,
=0.7,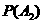 =0.6,
=0.6,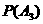 =0.5. --- 2分
=0.5. --- 2分
(1) 至少有一人命中目标的概率为
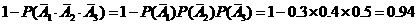 ; ---
4分
; ---
4分
(2) 恰有两人命中目标的概率为
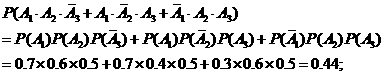 --- 4分
--- 4分
(3) 所求概率为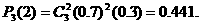 --- 4分
--- 4分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com