
题目列表(包括答案和解析)
2.若奇函数f(x)=kax-ax(a>0且a≠1)在R上是增函数,则g(x)=loga()的大致图象是( )
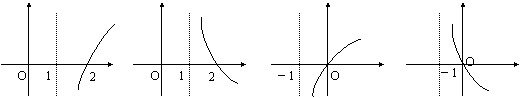
A B C D
1.若f(x)和g(x)都是定义在R上的函数,且均存在反函数,则函数f[g(x)]的反函数为( )
A.f-1[g-1(x)] B.f-1[g(x)] C.g-1[f-1(x)] D.g-1[f(x)]
(17) (本小题满分12分)在△ABC中,a,b,c分别为角A,B,C的对边,且a,b,c成等比数列.(I)求∠B的范围;(II)求y=2sin2B+sin(2B+)的取值范围.
解:(1)因为a,b,c成等比数列,所以b2=ac.
根据余弦定理,得cosB==≥=.
又因为0<B<,所以0<B≤.
所以∠B的范围是(0,].
(2)y=2sin2B+sin(2B+)=1-cos2B+sin2Bcos+cos2Bsin
=1+sin2Bcos-cos2Bsin=1+sin(2B-).
因为0<B≤,所以-<2B-≤,所以-<sin(2B-)≤1,所以<y≤2.
所以y=2sin2B+sin(2B+)的取值范围是(,2].
 (18)(本小题满分14分)如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD的中点.
(18)(本小题满分14分)如图,在多面体ABCDE中,AE⊥面ABC,BD∥AE,且AC=AB=BC=BD=2,AE=1,F为CD的中点.
(I)求证:EF⊥面BCD;
(II)求多面体ABCDE的体积;
(III)求面CDE与面ABDE所成的二面角的余弦值.
解:(I)取BC中点G,连FG,AG.
因为AE⊥面ABC,BD∥AE,所以BD⊥面ABC.
又AGÌ面ABC,所以BD⊥AG.
又AC=AB,G是BC的中点,所以AG⊥BC,所以AG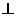 平面BCD.
平面BCD.
又因为F是CD的中点且BD=2,所以FG∥BD且FG=BD=1,所以FG∥AE.
又AE=1,所以AE=FG,所以四边形AEFG是平行四边形,所以EF∥AG,所以EF⊥面BCD.
 (II)设AB中点为H,则由AC=AB=BC=2,可得CH⊥AB且CH=.
(II)设AB中点为H,则由AC=AB=BC=2,可得CH⊥AB且CH=.
又BD∥AE,所以BD与AE共面.
又AE⊥面ABC,所以平面ABDE⊥平面ABC.
所以CH⊥平面ABDE,即CH为四棱锥C-ABDE的高.
故四棱锥C-ABDE的体积为VC-ABDE=SABDE·CH=[(1+2)×2×]=.
(III)过C作CK⊥DE于K,连接KH.
由三垂线定理的逆定理得KH⊥DE,所以∠HKC为二面角C-DE-B的平面角.
易知EC=,DE=,CD=2.
由S△DCE=×2×=×CK,可得CK=.
在Rt△CHK中,sin∠HKC==,所以cos∠HKC=,
所以面CDE与面ABDE所成的二面角的余弦值为.
(19)(本小题满分14分)某空调器厂为了规范其生产的空调器的市场营销,在一个地区指定一家总经销商,规定经总销商之间不得“串货”(即一个地区的总经销商不得向其他地区销售该品牌空调器).经空调器厂和各地区总经销商联合市场调查,预计今年的七月份(销售旺季),市场将需求售价为1800元/台的P型空调器200万台,但该厂的生产能力只有150万台.为了获得足够的资金组织生产,该空调器厂规定,每年的销售旺季前预付货款的总经销商在旺季将获得供货优待.以东部地区为例,今年的7月份市场将需求P型空调器10万台,如果东部地区的总经销商在2月1日将10万台P型空调器的货款全部付清,空调器厂按1500元/台的价格收取货款,并在7月1日保证供货;每推迟一个月打入货款,每台空调器的价格将增加6元,并且供货量将减少2%.已知银行的月利率为0.5%.
(I)就P型空调器的进货单价而言,总经销商在2月1日和7月1日打入货款,哪个划算?
(II)就东部地区经销P型空调器而言,总经销商在2月1日和7月1日打入货款,哪个划算?
(III)东部地区的小王7月1日用分期付款的方式购买了1台P型空调器,如果采用每月“等额还款”的方式从7月1日开始分6次付清,小王每一次的付款额约是多少?
(以下数据仅供参考:1.0054=1.020151,1.0055=1.025251,1.0056=1.030378,0.985=0.903921,0.986=0.885842,0.987=0.868126)
解 (I)2月1日打入货款,P型空调器的进货单价为1500元;7月1日打入货款,P型空调器的进货单价为1500+5×6=1530(元).
由于1500×(1+0.5%)5=1500×1.025251≈1537.88>1530,
所以,就P型空调器的进货单价而言,经销商在7月1日打入货款划算.
(II)2月1日打入货款,东部地区经销P型空调器的利润是100000×(1800-1537.88)=26212000(元);
7月1日打入货款,东部地区经销P型空调器的台数是100000×(1-2%)5=90392.1≈90392,
利润为90392×(1800-1530)=24405840(元).
由于24405840<26212000,所以,就东部地区经销P型空调器而言,在2月1日打入货款最划算.
(III)设小王每个月的还款数额为x元,
则(1+1.005+1.0052+1.0053+1.0054)x=(1800-x)×1.0055,
即 x=1800×1.0055,
解得x===303.75(元).
答:小王每一次的付款额约是303.75元.
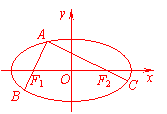
(20)(本小题满分14分)设椭圆+=1(a>b>0)的离心率为e,A为椭圆上一点,弦AB,AC分别过焦点F1,F2.
(I)若∠AF1F2=α,∠AF2F1=β,试用α,β表示椭圆的离心率e;
(II)设→=λ1→,→=λ2→,当A在椭圆上运动时,求证:λ1+λ2为定值.
解:(I)设F1(-c,0),F2(c,0).在△AF1F2中,由正弦定理得
==,
 即 |AF1|=,|AF2|=,
即 |AF1|=,|AF2|=,
所以 2a=|AF1|+|AF2|=+
=2c(+)=2c·,
得 e=.
(II)设A(x0,y0),B(x1,y1),C(x2,y2).
①当y0=0时,λ1+λ2=2=;当AB或AC与x轴垂直时,λ1+λ2=.
②当AB,AC都不与x轴垂直且y0≠0时,AC的方程为y=(x-c),
由消x得[b2(x0-c)2+a2y]y2+2b2y0(x0-c)y+c2b2y-a2b2y=0.
由韦达定理得 y2y0=,
所以 y2=,
所以 λ2==-=- ,
同理可得 λ1==-=-,
故 λ1+λ2=-[+]
=-===,
综上可知 λ1+λ2=.
(21)(本小题满分16分)设函数f(x)=x3+x2+x+5(a,b∈R,a>0)的定义域为R.当x=x1时取得极大值,当x=x2时取得极小值.
(I)若x1<2<x2<4,求证:函数g(x)=ax2+bx+1在区间(-∞,-1]上是单调减函数;
(II)若|x1|<2,|x1-x2|=4,求实数b的取值范围.
解法一 f '(x)=ax2+(b-1)x+1.
因为f(x)当x=x1时取得极大值,当x=x2时取得极小值.
所以f '(x)=ax2+(b-1)x+1=0的两根为x1,x2,且x1<x2.
(Ⅰ)由题知,f '(x)=0的两个根x1,x2满足x1<2<x2<4,
当且仅当
所以16a+4b>3>3(4a+2b),得->-1.
因为函数g(x)=ax2+bx+1在区间(-∞,-)上是单调减函数,
所以函数g(x)=ax2+bx+1在区间(-∞,-1]上是单调减函数;
(Ⅱ)因为方程ax2+(b-1)x+1=0的两个根x1,x2(x1<x2),且x1·x2=>0,所以x1,x2同号.
又|x1-x2|==4,所以(b-1)2=16a2+4a.③
若-2<x1<0,则-2<x1<x2<0,则|x1-x2|<2,与|x1-x2|=4矛盾,
所以0<x1<2,则所以4a+1<2(1-b),
结合③得(4a+1)2<4(1-b)2=4(16a2+4a),解得a>或-a<.结合a>0,得a>.
所以2(1-b)>4a+1>,得b<.
所以实数b的取值范围是(-∞,).
解法二 f'(x)=ax2+(b-1)x+1.
(Ⅰ)由题知,f'(x)=0的两个根x1,x2满足x1<2<x2<4,
当且仅当
由①得,-b>2a-.
因为a>0,所以->1-.③
由结合③,得->-1.
因为函数g(x)=ax2+bx+1在区间(-∞,-)上是单调减函数,
所以函数g(x)=ax2+bx+1在区间(-∞,-1)上是单调减函数;
(Ⅱ)因为x1·x2=>0,所以x1,x2同号.
由|x1|<2,得-2<x1<2.
若-2<x1<0,则-2<x1<x2<0,则|x1-x2|<2,与|x1-x2|=4矛盾,
所以0<x1<2,则x2>4.
所以得b<.
又因为|x1-x2|==4,所以(b-1)2=16a2+4a.
根据④⑤得得结合b<,得b<;
所以实数b的取值范围是(-∞,).
(11)在(1-)15的展开式中,系数最大的项是第 9 项.
(12)设{an}为等差数列,从{a1,a2,a3,…,a10}中任取4个不同的数,使这4个数仍成等差数列,则这样的等差数列最多有 24 个.
(13)已知命题p:不等式|x-m|+|x-1|>1的解集为R,命题q:f(x)=log(3+m)x是(0,+∞)上的增函数.若“p且q”是假命题,“p或q”是真命题,则实数m的取值范围是 (-3,-2)∪ [0,2] .
 (14)将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值是 .
(14)将一张画有直角坐标系的图纸折叠一次,使得点A(0,2)与点B(4,0)重合.若此时点C(7,3)与点D(m,n)重合,则m+n的值是 .
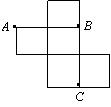 (15)如图,是一个无盖正方体盒子的表面展开图,A,B,C为其上的三个点,则在正方体盒子中,∠ABC等于 60o .
(15)如图,是一个无盖正方体盒子的表面展开图,A,B,C为其上的三个点,则在正方体盒子中,∠ABC等于 60o .
(16)有下列命题:
①G=(G≠0)是a,G,b成等比数列的充分非必要条件;
②若角α,β满足cosαcosβ=1,则sin(α+β)=0;
③若不等式|x-4|+|x-3|<a的解集非空,则必有a≥1;
④函数y=sinx+sin|x|的值域是[-2,2].
其中正确命题的序号是 ①②③④ .(把你认为正确的命题的序号都填上)
(1)设集合M={θ|θ=,k∈Z},N={x|cos2x=0,x∈R},P={α|sin2α=1,α∈R},则下列关系式中成立的是中国数学教育网 ( A )
(A)P,\d\fo0 ((N,\d\fo0 ((M (B)P=N,\d\fo0 ((M (C)P,\d\fo0 ((N=M (D)P=N=M
(2)下列四个函数中,值域是(-∞,-2]的一个函数是 ( D )
(A)y=-2x+1(x>) (B)y=-(x+1)2-2(-1≤x≤0)
(C)y=x+(x<-1) (D)y=log0.5(x++1)(x>1)
(3)若实数m,n满足<<0,则下列结论中不正确的是 ( D )
(A)m2<n2 (B)mn<n2 (C)+>2 (D)|m|+|n|>|m+n|
(4)要得到函数y=cot(-3x)的图象,可将y=tan3x的图象 ( B )
(A)向右平移个单位 (B)向左平移个单位 (C)向右平移个单位 (D)向左平移个单位
(5)已知直线m,n和平面α,则m∥n的一个必要不充分条件是 ( D )
(A)m∥α,n∥α (B)m⊥α,n⊥α (C)m∥α,n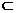 α (D)m,n与α所成角相等
α (D)m,n与α所成角相等
(6)已知向量a=(2cosα,2sinα),b=(3cosβ,3sinβ),a与b的夹角为60o,则直线xcosα-ysinα+1=0与圆(x-cosβ)2+(y+sinβ)2=1的位置关系是 ( C )
(A)相切 (B)相交 (C)相离 (D)随α,β的值而定
(7)已知x,y满足约束条件则z=2x+4y的最小值为 ( D )
(A)10 (B)-10 (C)6 (D)-6
(8)进入21世纪,肉食品市场对家禽的需求量大增,发展家禽养殖业成了我国一些地区发展农村经济的一个新举措.下列两图是某县2000-2005年家禽养殖业发展规模的统计结果,那么,此县家禽养殖数最多的年份是 ( B )
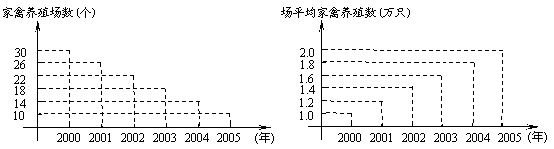
(A)2000年 (B)2001年 (C)2003年 (D)2004年
(9)已知椭圆+=1上有n个不同的点P1,P2,P3,…,Pn.设椭圆的右焦点为F,数列{|PnF|}是公差大于的等差数列,则n的最大值为 ( B )
(A)2007 (B)2006 (C)1004 (D)1003
(10)以正方体ABCD-A′B′C′D′的任意三个顶点为顶点作三角形,从中随机取出两个三角形,则这两个三角形共面的概率为 ( D)
(A) (B) (C) (D)
第Ⅱ卷(非选择题共100分)
(19) (本小题满分12分)
设函数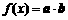 ,其中向量
,其中向量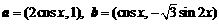 ,
, .
.
(Ⅰ)求函数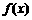 的单调减区间;
的单调减区间;
(Ⅱ)若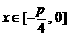 ,求函数
,求函数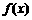 的值域;
的值域;
(Ⅲ)若函数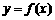 的图象按向量
的图象按向量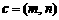
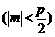 平移后得到函数
平移后得到函数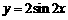 的图象,求实数
的图象,求实数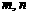 的值.
的值.
(20) (本小题满分12分)
在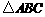 中,
中,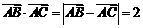 .
.
(Ⅰ)求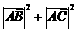 的值;
的值;
(Ⅱ)当 的面积最大时,求
的面积最大时,求 的大小.
的大小.
(21) (本小题满分14分)
设函数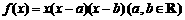 .
.
(Ⅰ)若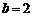 ,证明函数
,证明函数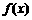 有两个不同的极值点
有两个不同的极值点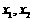 ,并且
,并且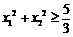 ;
;
(Ⅱ)若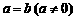 ,且当
,且当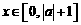 时,
时,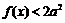 恒成立,求
恒成立,求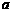 的取值范围.
的取值范围.
(22) (本小题满分14分)
某市电信宽带私人用户月收费标准如下表:
|
方案 |
类 别 |
基本费用 |
超时费用 |
|
甲 |
包月制 |
70元 |
|
|
乙 |
有限包月制(限60小时) |
50元 |
0.05元/分钟(无上限) |
|
丙 |
有限包月制(限30小时) |
30元 |
0.05元/分钟(无上限) |
假定每月初可以和电信部门约定上网方案.
(Ⅰ)若某用户每月上网时间为66小时,应选择 ▲ 方案最合算;
(Ⅱ)王先生因工作需要在家上网,所在公司预测其一年内每月的上网时间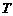 (小时)与月份
(小时)与月份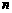 的函数关系为
的函数关系为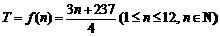 .若公司能报销王先生全年上网费用,问公司最少会为此花费多少元?
.若公司能报销王先生全年上网费用,问公司最少会为此花费多少元?
(Ⅲ)一年后,因公司业务变化,王先生每月的上网时间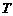 (小时)与月份
(小时)与月份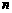 的函数关系为
的函数关系为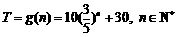 .假设王先生退休前一直从事此项业务,公司在花费尽量少的前提下,除为其报销每月的基本费用外,对于所有的超时费用,公司考虑一次性给予补贴
.假设王先生退休前一直从事此项业务,公司在花费尽量少的前提下,除为其报销每月的基本费用外,对于所有的超时费用,公司考虑一次性给予补贴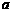 元,试确定最合理的
元,试确定最合理的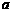 的值,并说明理由.
的值,并说明理由.
(23) (本小题满分14分)
已知函数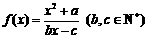 ,并且
,并且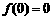 ,
,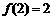 ,
,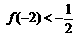 .
.
(Ⅰ)求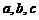 的值;
的值;
(Ⅱ)是否存在各项均不为零的数列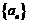 ,满足
,满足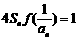 (
(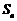 为数列
为数列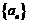 的前
的前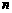 项和).若有,写出数列的一个通项公式
项和).若有,写出数列的一个通项公式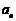 ,并说明满足条件的数列
,并说明满足条件的数列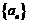 是否唯一确定;若无,请说明理由.
是否唯一确定;若无,请说明理由.
江苏省苏州市部分重点中学2006届高三期中考试试卷
(13) 若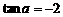 ,则
,则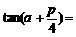 ▲ .
▲ .
(14) 函数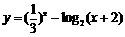 在区间
在区间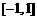 上的最大值为 ▲ .
上的最大值为 ▲ .
(15) 已知平面向量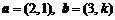 ,若
,若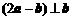 ,则实数
,则实数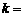 ▲ .
▲ .
(16) 已知集合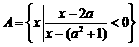 ,
,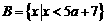 ,若
,若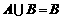 ,则实数
,则实数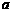 的取值范围是
▲ .
的取值范围是
▲ .
(17) 已知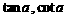 分别是关于
分别是关于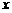 的二次方程
的二次方程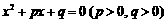 的两实根的等差中项和等比中项,则
的两实根的等差中项和等比中项,则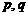 满足的关系式为 ▲ .
满足的关系式为 ▲ .
(18) 若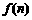 为
为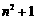 的各位数字之和
的各位数字之和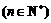 .如:因为
.如:因为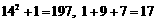 ,所以
,所以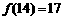 .记
.记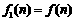 ,
,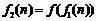 ,……,
,……,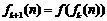 ,
,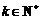 ,则
,则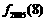 = ▲ .
= ▲ .
(1)已知平面向量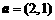 ,
,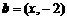 ,且
,且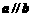 ,则
,则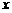 的值为 ( )
的值为 ( )
A.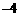 B.
B.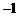 C.1 D.4
C.1 D.4
(2)已知集合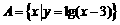 ,
,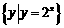 ,则
,则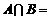 ( )
( )
A.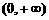 B.
B.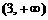 C.
C.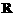 D.
D.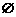
(3)已知函数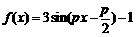 ,则下列命题正确的是 ( )
,则下列命题正确的是 ( )
A.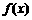 是周期为1的奇函数 B.
是周期为1的奇函数 B.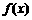 是周期为2的偶函数
是周期为2的偶函数
C.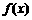 是周期为1的非奇非偶函数 D.
是周期为1的非奇非偶函数 D.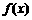 是周期为2的非奇非偶函数
是周期为2的非奇非偶函数
(4)设等差数列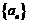 的前
的前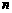 项和为
项和为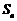 ,若
,若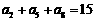 ,则
,则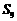 等于 ( )
等于 ( )
A.18 B.36 C.45 D.60
(5)函数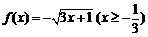 的反函数 ( )
的反函数 ( )
A.在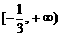 上单调递增 B.在
上单调递增 B.在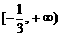 上单调递减
上单调递减
C.在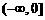 上单调递增 D.在
上单调递增 D.在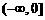 上单调递减
上单调递减
(6)设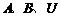 均为非空集合,且满足
均为非空集合,且满足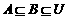 ,则下列各式中错误的是 ( )
,则下列各式中错误的是 ( )
A.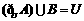 B.
B.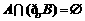
C.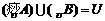 D.
D.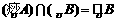
(7)命题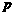 :
: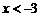 是
是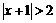 的充分不必要条件;
命题
的充分不必要条件;
命题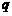 :在
:在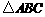 中,如果
中,如果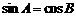 ,那么
,那么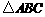 为直角三角形.则 ( )
为直角三角形.则 ( )
A.“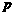 或
或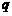 ”为假 B.“
”为假 B.“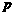 且
且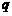 ”为真 C.
”为真 C.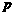 假
假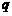 真 D.
真 D.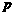 真
真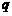 假
假
(8)设函数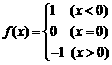 ,则当
,则当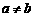 时,
时,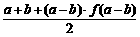 的值应为 ( )
的值应为 ( )
A. B.
B.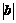 C.
C.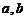 中的较小数 D.
中的较小数 D.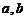 中的较大数
中的较大数
(9)函数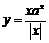
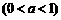 的图象的大致形状是 ( )
的图象的大致形状是 ( )
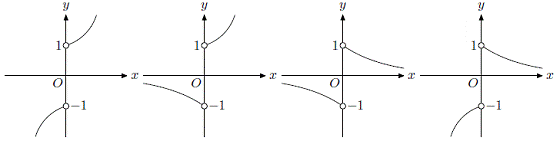
A B C D
(10)在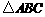 中,
中,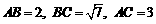 ,则
,则 边上的高为 ( )
边上的高为 ( )
A.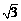 B.
B.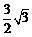 C.1 D.
C.1 D.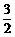
(11)已知函数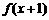 为奇函数,函数
为奇函数,函数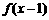 为偶函数,且
为偶函数,且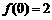 ,则
,则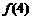 = ( )
= ( )
A.2 B.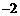 C.4 D.
C.4 D.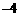
(12)为了稳定市场,确保农民增收,某农产品的市场收购价格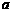 与其前三个月的市场收购价格有关,且使
与其前三个月的市场收购价格有关,且使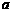 与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
与其前三个月的市场收购价格之差的平方和最小.若下表列出的是该产品前6个月的市场收购价格:
|
月份 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
价格(元/担) |
68 |
78 |
67 |
71 |
72 |
70 |
|
则7月份该产品的市场收购价格应为 ( )
A.69元 B.70元 C.71元 D.72元
第Ⅱ卷(非选择题 共90分)
19. 直线
直线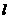 经过抛物线
经过抛物线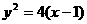 的焦点,且与准线成30
的焦点,且与准线成30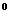 角,则直线
角,则直线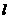 的斜截式方程是
的斜截式方程是
18.已知双曲线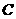 :
: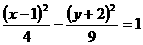 ,给出以下四个命题:
,给出以下四个命题:
① 双曲线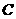 的渐近线方程是
的渐近线方程是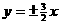 ;
;
② 直线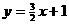 与双曲线
与双曲线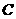 只有一个交点;
只有一个交点;
③ 将双曲线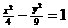 向左平移一个单位,并向上平移两个单位,可以得到双曲线
向左平移一个单位,并向上平移两个单位,可以得到双曲线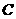 ;
;
④ 双曲线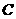 的一个焦点到一条渐近线的距离为3。
的一个焦点到一条渐近线的距离为3。
 其中所有正确命题的序号是
其中所有正确命题的序号是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com