
题目列表(包括答案和解析)
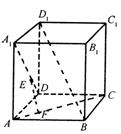
7. 在正方体ABCD-A1B1C1D1中,E、F分别在A1D、AC上,且A1E=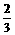 A1D,AF=
A1D,AF=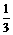 AC,则
AC,则
A.EF至多与A1D、AC之一垂直 B.EF是A1D、AC公垂线
C.EF与BD1相交 D.EF与BD1异面
6. 设z∈C,z=(1-i)2+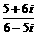 ,则(1+z)7展开式的第5项是
,则(1+z)7展开式的第5项是
 A.35i B.-21i C.21 D.35
A.35i B.-21i C.21 D.35
5. 设函数f(x)=1ogax(a>0且a≠1),若f(x1·x2·x3·…·x2006)=50,则f(x12)+f(x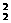 )+f(x
)+f(x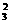 )+…+f(x
)+…+f(x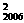 )的值等于
)的值等于
A.2500 B.50 C.100 D.2log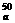
4.若直线mx+2ny-4=0(m,n∈R)始终平分圆x2+y2-4x-2y-4=0的周长,则m·n的取值范围是
A.(0,1) B.(0,1] C.(-∞,1) D.(-∞,1]
3.若a、b、c是互不相等的实数,且a、b、c成等差数列,c、a、b成等比数列,则a:b:c等于
A.(-2)∶1∶4 B.1∶2∶3 C.2∶3∶4 D.(-1) ∶1∶3
2.已知cos31°=m,则sin239°·tan149°的值是
A.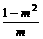 B.
B.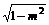 C.
C.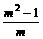 D.-
D.-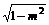
1.设集合U={(x,y)|x∈R,y∈R},A={(x,y)|2x-y+m>0},B={(x,y)|x+y-n≤0},那么点P(2,3)∈A ∩(CUB)的充要条件是
A.m>1-且n<5 B.m<-1且n<5
C.m>-1且n>5 D.m<-1且n>5
21.(本小题满分14分)
已知双曲线C的中心在原点,对称轴为坐标轴,其一条渐近线方程是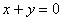 ,且双曲线C过点
,且双曲线C过点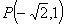 .
.
(1)求此双曲线C的方程;
(2)设直线L过点A(0,1),其方向向量为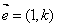 (
(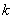 >0),令向量
>0),令向量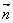 满足
满足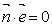 .问:双曲线C的右支上是否存在唯一一点B,使得
.问:双曲线C的右支上是否存在唯一一点B,使得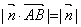 .若存在,求出对应的
.若存在,求出对应的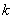 的值和B的坐标;若不存在,说明理由.
的值和B的坐标;若不存在,说明理由.
20.(本小题满分14分)
已知函数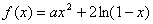 (
(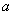 为实数).
为实数).
(1)若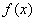 在[-3,-2 )上是增函数,求实数
在[-3,-2 )上是增函数,求实数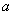 的取值范围;
的取值范围;
(2)设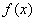 的导函数
的导函数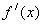 满足
满足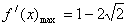 ,求出
,求出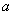 的值.
的值.
19.(本小题满分14分)
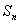 是正数数列
是正数数列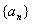 的前n项的和,数列S12,S22、……、Sn2 ……是以3为首项,以1为公差的等差数列;数列
的前n项的和,数列S12,S22、……、Sn2 ……是以3为首项,以1为公差的等差数列;数列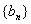 为无穷等比数列,其前四项的和为120,第二项与第四项的和为90.
为无穷等比数列,其前四项的和为120,第二项与第四项的和为90.
(1)求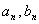 ;
;
(2)从数列{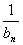 }中依次取出部分项组成一个无穷等比数列
}中依次取出部分项组成一个无穷等比数列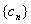 ,使其各项和等于
,使其各项和等于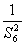 ,求数列
,求数列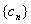 公比
公比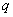 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com