
题目列表(包括答案和解析)
6. 已知函数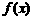 是定义在
是定义在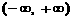 上的偶函数. 当
上的偶函数. 当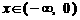 时,
时,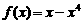 ,则 当
,则 当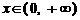 时,
时,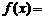 . txjy
. txjy
5. 已知圆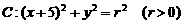 和直线
和直线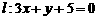 . 若圆
. 若圆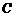 与直线
与直线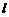 没有公共 点,则
没有公共 点,则 的取值范围是
. txjy
的取值范围是
. txjy
4. 不等式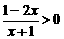 的解集是
. txjy
的解集是
. txjy
3. 函数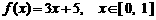 的反函数
的反函数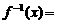 .
.
2. 方程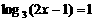 的解
的解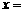 .
.
1. 计算: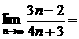 . txjy
. txjy
20.在平面直角坐标系中,O为坐标原点,已知点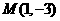 ,
,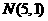 ,若点C满足
,若点C满足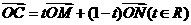 ,点C的轨迹与抛物线
,点C的轨迹与抛物线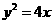 交于A、B两点;
交于A、B两点;
(1)求点C的轨迹方程;
(2)求证: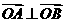 ;
;
(3)在x轴正半轴上是否存在一定点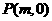 ,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
,使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
解:(1)设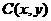 ,由
,由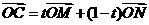 知,点C的轨迹为
知,点C的轨迹为 …2分
…2分
(2)由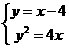 消y得:
消y得: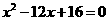
设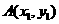 ,
,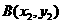 ,则
,则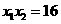 ,
,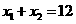 ………………………………5分
………………………………5分
所以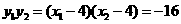 ,所以
,所以 ,于是
,于是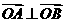 ………………7分
………………7分
(3)假设存在过点P的弦EF符合题意,则此弦的斜率不为零,设此弦所在直线的方程为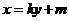
由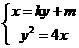 消x得:
消x得: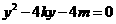 ,设
,设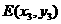 ,
,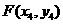 ,
,
则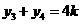 ,
,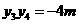 ……………………10分
……………………10分
因为过点P作抛物线的弦的长度是原点到弦的中点距离的2倍,所以 即
即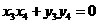
所以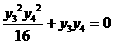 得
得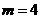 ,所以存在
,所以存在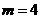 ……………………………………14分
……………………………………14分
19.已知函数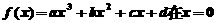 处取得极值,曲线
处取得极值,曲线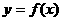 过原点O(0,0)和点
过原点O(0,0)和点
P(-1,2),若曲线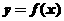 在点P处的切线l与直线
在点P处的切线l与直线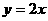 的夹角为45°,且l的倾斜角为钝角.
的夹角为45°,且l的倾斜角为钝角.
(Ⅰ)求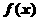 的解析式;
的解析式;
(Ⅱ)若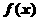 在区间[2m-1,m+1]上是增函数,求m的取值范围.
在区间[2m-1,m+1]上是增函数,求m的取值范围.
解:(I)∵曲线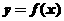 过原点,所以d=0;
过原点,所以d=0;
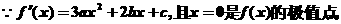
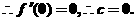
∵过点P(-1,2)的切线l的斜率为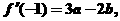
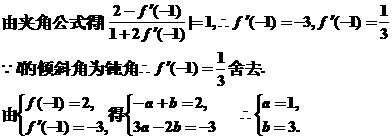
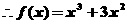 (a,b,c,d每求对一个得2分,共8分)
(a,b,c,d每求对一个得2分,共8分)
(II)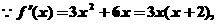
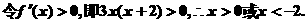

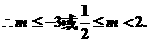 ----------14分
----------14分
18.经统计,某大医院一个结算窗口每天排队结算的人数及相应的概率如下:
|
排队人数 |
0-5 |
6-10 |
11-15 |
16-20 |
21-25 |
25人以上 |
|
概 率 |
0.1 |
0.15 |
0.25 |
0.25 |
0.2 |
0.05 |
(1)每天不超过20人排队结算的概率是多少?
(2)一周7天中,若有3天以上(含3天)出现超过15人排队结算的概率大于0.75,医院就需要增加结算窗口,请问该医院是否需要增加结算窗口?
解:(1)每天不超过20人排队结算的概率为:P=0.1+0.5+0.25+0.25=0.75,即不超过20人排队结算的概率为0.75.------------4分
(2)每天超过15人排队结算的概率为:0.25+0.2+0.25=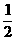 ,-------------8分
,-------------8分
一周7天中,没有出现超过15人排队结算的概率为C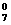 (
(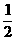 )7;
)7;
一周7天中,有一天出现超过15人排队结算的概率为C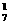 (
(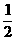 )(
)(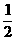 )7;
)7;
一周7天中,有二天出现超过15人排队结算的概率为C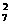 (
(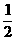 )2(
)2(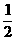 )5;
)5;
所以有3天或3天以上出现超过15人排队结算的概率为:
1-[C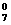 (
(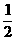 )7+C
)7+C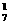 (
(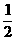 )(
)(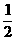 )6+C
)6+C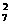 (
(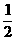 )2(
)2(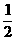 )5]=
)5]=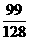 >0.75,---------13分
>0.75,---------13分
所以,该医院需要增加结算窗口.--------------14分
17.已知正四棱柱ABCD-A1B1C1D1底面边长为2,AA1=4,点E在AA1上,AC与BD交于点O;
(1)若EA=2,求证:A1C//平面EBD;
(2)若EA=3,求二面角A-DE-B的正切值;
(3)在AA1上是否存在点E,使异面直线EB与AC所成的角为300?若存在,试确定E点的位置,否则说明理由。
解:(1)证明A1C//EO即可;
(2)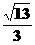
(3)不存在,可用向量法;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com