
题目列表(包括答案和解析)
2.已知l,m为两条直线,则下列条件中可以判断平面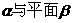 平行的是 ( )
平行的是 ( )
A.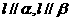 B.
B.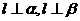
C.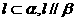 D.
D.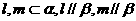
1.已知集合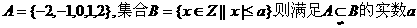 可以取的一个值为 ( )
可以取的一个值为 ( )
A.0 B.1
C.2 D.3
22.(理)(14分)已知数列{an}满足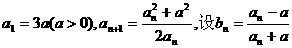
(1)求数列{bn}的通项公式;
(2)设数列{bn}的前项和为Sn,试比较Sn与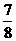 的大小,并证明你的结论.
的大小,并证明你的结论.
(文)数列{an}的前n项和Sn,已知Sn是各项为正数的等比数列,试比较
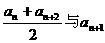 的大小,证明所得的结论.
的大小,证明所得的结论.
21.(12分)椭圆中心为原点O,焦点F1,F2在x轴上,F1为左焦点,过F1作斜率为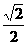 的直线交椭圆于
的直线交椭圆于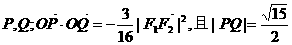 求椭圆方程.
求椭圆方程.
20.(12分)某项希望工程准备兴办一所分校,投资1200万用于硬件建设.为了考虑社会效益和经济利益,对该地区教育市场进行调查,得出一组数据列表(以班为单位)如下:
|
|
班级学生数 |
配备教师数 |
硬件建设(万元) |
教师年薪(万元/人) |
|
初中 |
60 |
2.0 |
28 |
1.2 |
|
高中 |
40 |
2.5 |
58 |
1.6 |
根据有关规定,除书本费、办公费外,初中生每年可收取学费600元,高中生每年可收取学费1500元,因生源和环境等条件限制,办学规模以20对30个班为宜.根据以上情况,请你合理规划办学规模使年利益最大,最大利润是多少万元?(利润=学费收入-年薪支出)
19.(12分)解不等式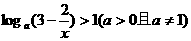 .
.
18.(12分)已知函数f(x)是定义在R上的周期函数,周期为5,函数y=f(x)在[-1,1]上是奇函数,且在[0,1]上是一次函数,在[1,4]上是二次函数,且在x=2时,取最大值5.
(1)求f(1)+f(4)的值;
(2)求y=f(x)在[1,4]上的解析式;
(3)求y=f(x)在[4,9]上的解析式.
17.(12分)已知函数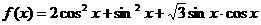
(1)求函数f(x)的最小正周期和最大值;
(2)作出函数 上的图象
上的图象
16.已知f(x)=4x-(k+1)·2x+2,当x∈R时,f(x)恒为正值,则k的取值范围是
15.设x1, x2∈R定义运算×:x1×x2=(x1+x2)2-(x1-x2)2,若x≥0,常数m>0,则动点
P(x,
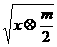 的轨迹方程是
的轨迹方程是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com