
题目列表(包括答案和解析)
10.(山东省实验中学2006)
已知函数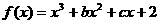 在
在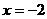 和
和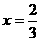 处取得极值,
处取得极值,
(1)确定函数 的解析式;
的解析式;
(2)求函数 的单调区间。
的单调区间。
解:(1)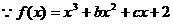
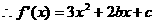 2分
2分
又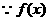 在
在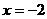 和
和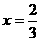 处取得极值
处取得极值
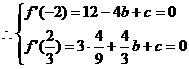 4分
4分
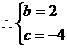
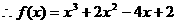 6分
6分
(2)由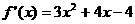
若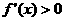 则
则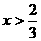 或
或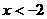 8分
8分
若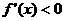 则
则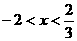 9分
9分
∴函数 的单调减区间为[-2,
的单调减区间为[-2,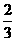 ] 10分
] 10分
函数 的单调增区间为
的单调增区间为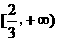 和
和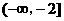 12分
12分
9.(潜山中学)已知函数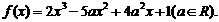
(I)求函数f(x)的单调区间; (II)设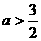 ,求函数f(x)在[1,2]上的最小值.
,求函数f(x)在[1,2]上的最小值.
解:(I)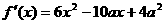
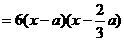
当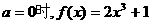 是R上的增函数. ………………2分
是R上的增函数. ………………2分
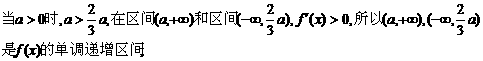
在区间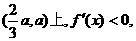 所以此区间是
所以此区间是 的单调递减区间;……4分
的单调递减区间;……4分
当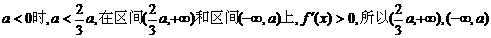
是 的单调递增区间;
的单调递增区间;
在区间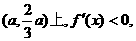 所以此区间是
所以此区间是 的单调递减区间;…………6分
的单调递减区间;…………6分
(II)因为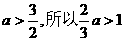 .
.
①当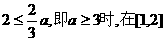 上函数
上函数 为增函数,
为增函数, 的最小值为f(1),
的最小值为f(1),
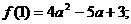 ………………8分
………………8分
②当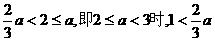 ,根据
,根据 的单调性,
的单调性, 的最小值为f(1),
的最小值为f(1),
f(2)中的值小的一个,
因为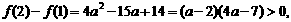 所以最小值为
所以最小值为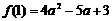 ;
;
………………10分
③当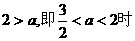 ,根据
,根据 的单调性,
的单调性, 的最小值为f(1),f(a)中的值小的一个,
的最小值为f(1),f(a)中的值小的一个,
因为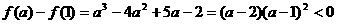 ,
,
所以最小值为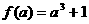 ;
;
综上,当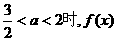 的最小值为
的最小值为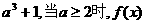 的最小值为
的最小值为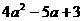 .
.
8.(临沭县实验中学1)
已知函数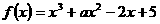 .
.
⑴若函数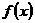 在
在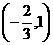 上单调递减,在
上单调递减,在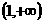 上单调递增,求实数
上单调递增,求实数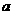 的值;
的值;
⑵求证:当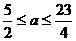 时,
时,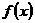 在
在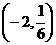 上单调递减.
上单调递减.
解:⑴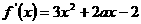 ……………………………………1分
……………………………………1分
∵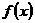 在
在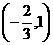 上单调递减,在
上单调递减,在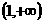 上单调递增,
上单调递增,
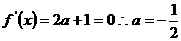 ……………………………………4分
……………………………………4分
⑵要使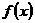 在
在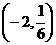 上单调递减,则对
上单调递减,则对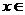
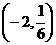 总有
总有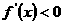 ………6分
………6分
∵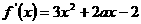 ,∴当
,∴当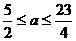 时,即
时,即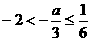 ,
,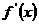 在
在
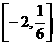 上的最大值为
上的最大值为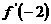 或
或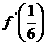 …………………………8分
…………………………8分
∵当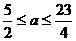 时,
时,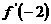 =10-4
=10-4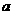 ≤10
≤10 ,
,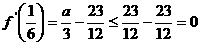 ………………………11分
………………………11分
∴对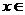
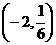 总有
总有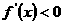
∴当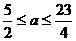 时,
时,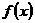 在
在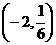 上单调递减 ………………………12分
上单调递减 ………………………12分
7.(临沭县实验中学2)
已知函数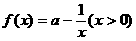
(1)求证:函数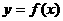 在(0,
在(0, )上是增函数;
)上是增函数;
(2)若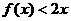 在[1,
在[1, )上恒成立,求实数a的取值范围;
)上恒成立,求实数a的取值范围;
(3)若函数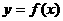 在
在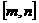 上的值域是
上的值域是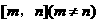 ,求实数a的取值范围。
,求实数a的取值范围。
解:(1)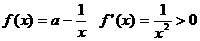
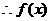 在(0,
在(0, )上为增函数 2分
)上为增函数 2分
(2)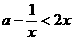 在(1,
在(1, )上恒成立
)上恒成立
设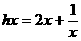
则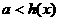 在(1,
在(1, )上恒成立
)上恒成立
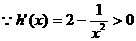
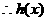 在[1,
在[1, )上单调递增
)上单调递增
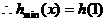 5分
5分
故 即
即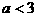
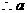 的取值范围为(
的取值范围为(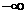 ,3) 7分
,3) 7分
(3)由题意知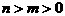 时,由(1)知
时,由(1)知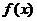 在(0,
在(0, )上单调递增
)上单调递增
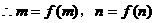 ,
,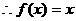 有两个不相等的正根
有两个不相等的正根
即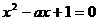 有两个不相等的正根m,n 10分
有两个不相等的正根m,n 10分
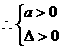
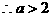 12分
12分
6.已知函数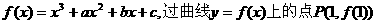 的切线方程为y=3x+1,且函数
的切线方程为y=3x+1,且函数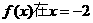 处有极值.
处有极值.
(Ⅰ)求 的表达式;(Ⅱ)求函数
的表达式;(Ⅱ)求函数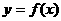 在[-3,1]上的最大值.
在[-3,1]上的最大值.
解:(1)由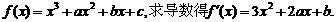
过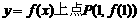 的切线方程为:
的切线方程为:
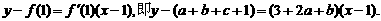 …………2分
…………2分
而过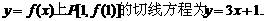
|
 …………4分
…………4分
∵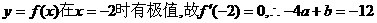 ③ ……5分
③ ……5分
由①②③得 a=2,b=-4,c=5.
∴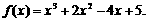 ………………7分
………………7分
(2)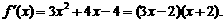
当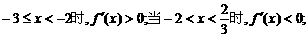
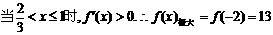 …………12分
…………12分
又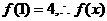 在[-3,1]上最大值是13. …………14分
在[-3,1]上最大值是13. …………14分

5.(本小题满分14分)函数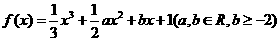 ,
,
当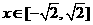 ,总有
,总有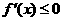 .
.
(1)求函数 的解析式;
的解析式;
(2)设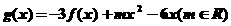 ,
,
求证:当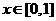 时,
时, 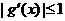 成立的充要条件是:
成立的充要条件是: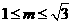
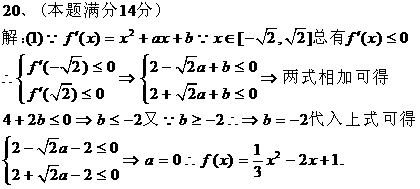
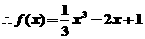

4.(杭州西湖高级中学)已知函数f(x)=(x2+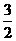 )(x+a)(a
)(x+a)(a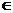 R)
R)
(1)若函数f(x)的图象上有与x轴平行的切线,求a的范围;
(2)若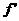 (-1)=0,(I)求函数f(x)的单调区间;
(-1)=0,(I)求函数f(x)的单调区间;
(II)证明对任意的x1、x2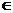 (-1,0),不等式|f(x1)-f(x2)|<
(-1,0),不等式|f(x1)-f(x2)|<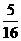 恒成立。
恒成立。
解: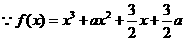 ,
,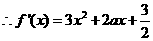
⑴ 函数
函数 的图象有与
的图象有与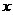 轴平行的切线,
轴平行的切线,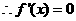 有实数解
有实数解
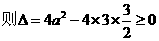 ,
,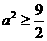 ,
,
所以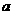 的取值范围是
的取值范围是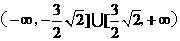
⑵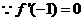 ,
,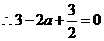 ,
,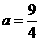 ,
,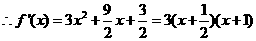
(Ⅰ)由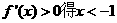 或
或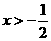 ;由
;由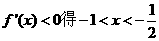
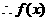 的单调递增区间是
的单调递增区间是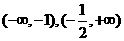 ;单调减区间为
;单调减区间为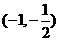
(Ⅱ)易知 的最大值为
的最大值为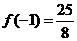 ,
, 的极小值为
的极小值为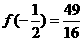 ,又
,又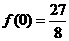
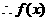 在
在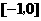 上的最大值
上的最大值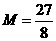 ,最小值
,最小值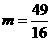
 对任意
对任意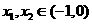 ,恒有
,恒有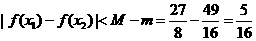
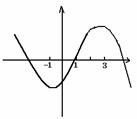
3.(06厦门双十中学高三数学质量检查试卷)
已知三次函数 的导函数为
的导函数为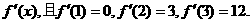
(1)求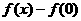 的表达式;
的表达式;
(2)若对任意的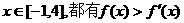 成立,求
成立,求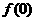 的取值范围.
的取值范围.
 解:(1)设
解:(1)设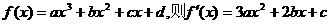 …………1分
…………1分
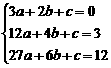 …………4分 ∴
…………4分 ∴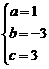
∴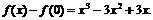 …………6分
…………6分
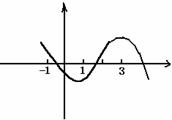 (2)
(2)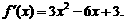 对任意的
对任意的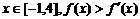
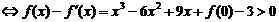
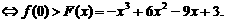 …………8分
…………8分
∵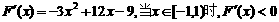 ;
;
当x=1时或3时,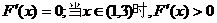 ;
;
当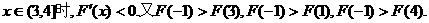
∴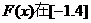 上的最大值为
上的最大值为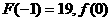 的取值范围是(19,+∞).……12分
的取值范围是(19,+∞).……12分
1.( 06年德阳中学)
已知f(x)=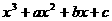 在x=1,x=
在x=1,x=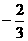 时,都取得极值。
时,都取得极值。
(1) 求a、b的值。
(2)
若对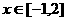 ,都有
,都有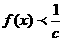 恒成立,求的取值范围。
恒成立,求的取值范围。
解:(1)由题意f/(x)=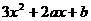 的两个根分别为1和
的两个根分别为1和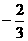
由韦达定理,得:1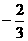 =
=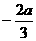 ,
,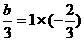
则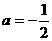 ,
,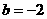
(2)由(1),有f(x)=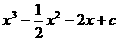 ,f/(x)=
,f/(x)=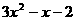
当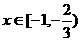 时,
时,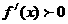 ,当
,当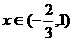 时,
时,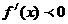 ,当
,当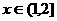 时,
时,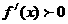 ,
,
当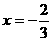 时,
时, 有极大值
有极大值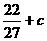 ,
,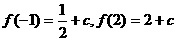 ,
,
∴ 当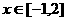 ,
, 的最大值为
的最大值为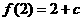
对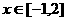 ,都有
,都有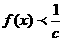 恒成立,∴
恒成立,∴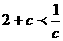 ,
,
解得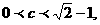 或
或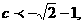
2 (06年云南省第一次高中毕业复习统一检测)
已知函数f(x)=ax3+bx2+cx+d在x=0处取得极值,曲线y=f(x)过原点O(0, 0)和点P(-1, 2),若曲线y=f(x)在P处的切线l与直线y=2x的夹角为45°,且l的倾角为钝角。
(Ⅰ)求f(x)的解析式;
(Ⅱ)若y=f(x)在区间 [2m-1, m+1] 上是增函数,求m的取值范围.

24.(无锡市辅仁高级中学)
函数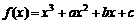 ,过曲线
,过曲线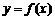 上的点
上的点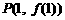 的切线方程为
的切线方程为
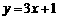
(1)若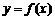 在
在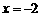 时有极值,求f (x)的表达式;
时有极值,求f (x)的表达式;
(2)在(1)的条件下,求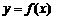 在
在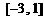 上最大值;
上最大值;
(3)若函数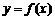 在区间
在区间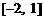 上单调递增,求b的取值范围.
上单调递增,求b的取值范围.
解:(1)

(2)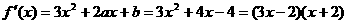
|
x |
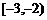 |
-2 |
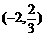 |
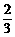 |
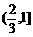 |
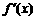 |
+ |
0 |
- |
0 |
+ |
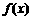 |
 |
极大 |
 |
极小 |
 |
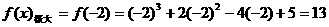
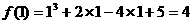
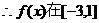 上最大值为13
上最大值为13
(3)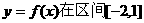 上单调递增
上单调递增
又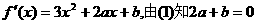
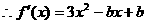
依题意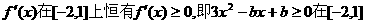 上恒成立.
上恒成立.
①在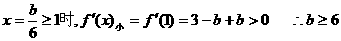
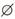 ②在
②在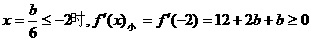
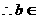
③在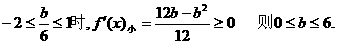
综合上述讨论可知,所求参数b取值范围是:b≥0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com