
题目列表(包括答案和解析)
21.(本小题满分12分)
已知函数f(x)=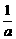 (3x-b)的图象过点A(1,2),B(2,5)
(3x-b)的图象过点A(1,2),B(2,5)
(1)求函数f-1(x)的解析式;
(2)记an=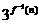 ,n∈N*,是否存在正数k,使得(1+
,n∈N*,是否存在正数k,使得(1+ )(1+
)(1+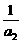 )…(1+
)…(1+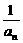 )≥k
)≥k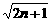 对
对
一切n∈N*均成立,若存在求出k的最大值,若不存在说明理由。
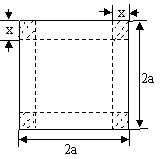
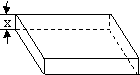
20.(本题满分12分)从边长2a的正方形铁片的四个角各截一个边长为x的正方形,然后拆
成一个无盖的长方体盒子,要求长方体的高度x与底面正方形边长的比不超过正常数t.
(1)把铁盒的容积V表示为x的函数,并指出其定义域;
(2)x为何值时,容积V有最大值.
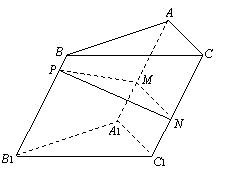
19.(本题满分12分) 如图,点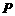 为斜三棱柱
为斜三棱柱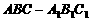 的侧棱
的侧棱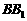 上一点,
上一点,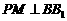
交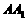 于点
于点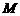 ,
,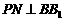 交
交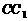 于点
于点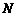 .
.
(1)求证: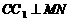 ;
;
(2)在任意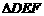 中有余弦定理:
中有余弦定理: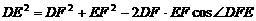 . 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
. 拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
18.(本小题满分12分)
口袋里装有大小相同的卡片八张,其中三张标有数字1,三张标有数字2,二张标
有数字3,第一次从口袋里任里任意抽取一张,放回口袋里后第二次再任意抽取一张,
记第一次与第二次取到卡片上数字之和为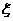 .
.
(1)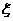 为何值时,其发生的概率最大?说明理由;
为何值时,其发生的概率最大?说明理由;
(2)求随机变量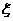 的期望E
的期望E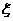 .
.
17.(本小题满分12分)
已知 、
、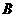 是
是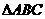 的两个内角,且
的两个内角,且 、
、 是方程
是方程 的两个实根,求
的两个实根,求 的取值范围.
的取值范围.
16.已知四个面都是直角三角形的三棱锥,其中三个面展开后构成一直角梯形ABCD,如图,AD⊥AB,AD⊥DC,AB=2,BC=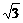 ,CD=1,则这个三棱锥外接球的表面积是__________(结果可含π).
,CD=1,则这个三棱锥外接球的表面积是__________(结果可含π).
15. 在
在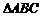 中,有命题①
中,有命题①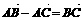 ;②
;②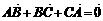 ;③若
;③若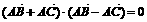 ,则
,则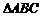 为等腰三角形;④若
为等腰三角形;④若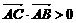 ,则
,则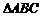 为锐角三角形.上述命题正确的是_____________ .
为锐角三角形.上述命题正确的是_____________ .
14.已知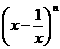 的展开式中所有二项式系数的和为512,则展开式中
的展开式中所有二项式系数的和为512,则展开式中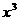 项的系数为_ ____.
项的系数为_ ____.
13.在数列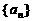 中,
中,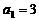 ,且对任意大于1的正整数
,且对任意大于1的正整数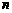 ,点
,点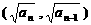 在直线
在直线
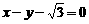 上,则
上,则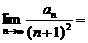 _____________.
_____________.
12.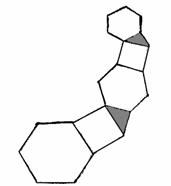 以边长为1的正六边形的一边为边向外作正方形,以正方形的一边为底向外作等腰直角三角形,再以等腰直角三角形一条直角边为边向外作正六边形,……,如此继续无限反复同一过程,则这些正六边形、正方形、等腰直角三角形面积之和为
( )
以边长为1的正六边形的一边为边向外作正方形,以正方形的一边为底向外作等腰直角三角形,再以等腰直角三角形一条直角边为边向外作正六边形,……,如此继续无限反复同一过程,则这些正六边形、正方形、等腰直角三角形面积之和为
( )
A.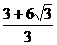 B.
B.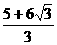
C.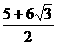 D.
D.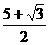
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com