
题目列表(包括答案和解析)
8.已知关于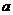 的方程
的方程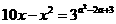 有两个不同的解,则
有两个不同的解,则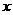 的取值范围是(
)。
的取值范围是(
)。
A.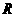 B.
B.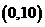
C.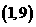 D.
D.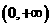
7.已知函数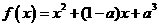 。又数列
。又数列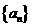 满足
满足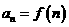
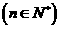 ,且
,且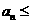
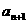 ,则正实数
,则正实数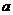 的取值范围是( )。
的取值范围是( )。
A.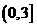 B.
B.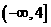 C.
C.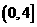 D.
D.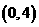
6.我们把“十位上的数字比百位、个位上的数字大,且千位上的数字比万位、百位上的数字大”的五位数叫“五位波浪数”,例如:“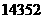 ”是一个五位波浪数。则从由
”是一个五位波浪数。则从由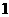 、
、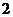 、
、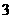 、
、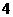 、
、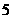 组成的没有重复数字的所有五位数中任意取一个数是五位波浪数的概率是(
)。
组成的没有重复数字的所有五位数中任意取一个数是五位波浪数的概率是(
)。
A.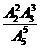 B.
B. 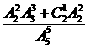
C. 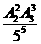 D.
D. 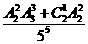
5.已知直线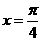 是函数
是函数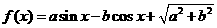
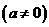 的图象的一条对称轴。则直线
的图象的一条对称轴。则直线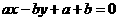 的倾斜角是( )。
的倾斜角是( )。
A.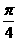 B.
B.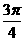 C.
C.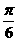 D.
D.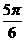
4.已知向量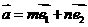 、
、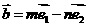 (其中
(其中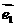 、
、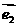 是不共线的向量,
是不共线的向量, 、
、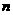
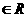 ),则
),则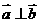 的充分不必要条件是( )。
的充分不必要条件是( )。
A. 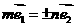 B.
B.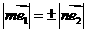
C. 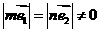 D.
D.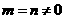 且
且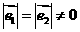
3.已知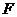 是抛物线
是抛物线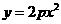
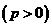 的焦点,
的焦点,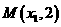 、
、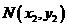 、
、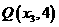 是这条抛物线上的三点,且
是这条抛物线上的三点,且 、
、 、
、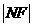 成等差数列。则
成等差数列。则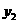 的值是( )。
的值是( )。
A.6 B.3 C.0 D.不能确定,与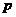 的值有关
的值有关
2.不等式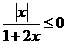 的解集是( )
的解集是( )
A.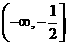 B.
B.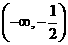
C.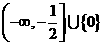 D.
D.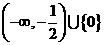
1.设有集合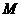 和
和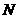 ,且
,且 、
、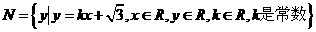 ,则集合
,则集合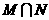 的真子集个数是( )。
的真子集个数是( )。
A.4 B.3 C.3或1 D.0
22、解:由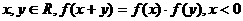 时,
时,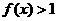 可得:
可得:
(1)令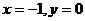 就得
就得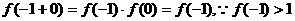 ,
,
∴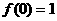 ; ……………………………………………2分
; ……………………………………………2分
若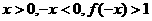 ,则
,则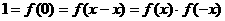 ,
,
∴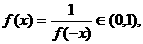 从而的当
从而的当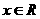 时,
时,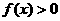 ;………4分
;………4分
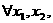 且
且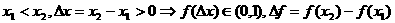
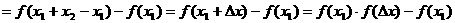
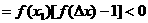 ;即得
;即得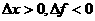 ;
;
∴函数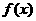 在
在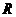 上是减函数.
…………………………6分
上是减函数.
…………………………6分
(2)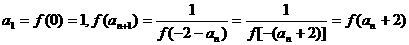
由函数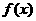 是
是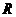 上单调函数,得
上单调函数,得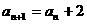 ,
………8分
,
………8分
得到数列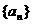 是等差数列,即:
是等差数列,即: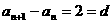 ,又
,又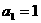
∴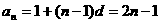 ,即通项公式为
,即通项公式为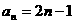 . ……10分
. ……10分
(3)当 ......
......
∴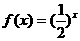 ,
,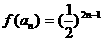 ,因此数列
,因此数列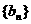 的通项公式为
的通项公式为
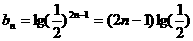 , ……………………………12分
, ……………………………12分
可以得出数列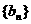 是以
是以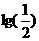 为首项,以
为首项,以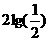 为公差的等差数列,
为公差的等差数列,
∴数列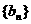 前
前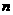 项和为:
项和为:
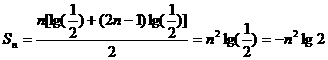 . …………14分
. …………14分
本资料由《七彩教育网》 提供!
21、解:猜想: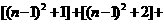 ……
……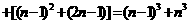
…………………………5分
证明: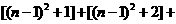 …
…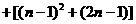
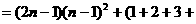 …
…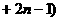 ……7分
……7分
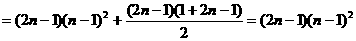
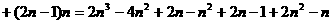
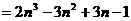 ……………………………10分
……………………………10分
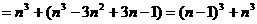 ;………11分
;………11分
∴证明的结论成立,即: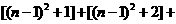
…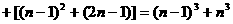 .
…………12分
.
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com