
题目列表(包括答案和解析)
20、解:在椭圆中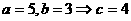 ,
,
∴得到两个焦点为: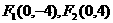 ,
,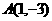 , ……2分
, ……2分
(1)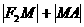 ≥
≥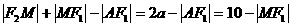 ,
,
当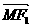 与
与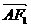 同向共线时取等号,即取最小值; ……4分
同向共线时取等号,即取最小值; ……4分
而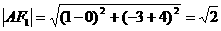 ,
,
∴当点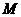 在椭圆上并在线段
在椭圆上并在线段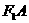 的延长线上时取得最小值,
的延长线上时取得最小值,
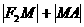 的最小值为
的最小值为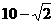 . …………………6分
. …………………6分
(2)当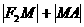 取得最小值时,点
取得最小值时,点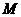 在直线
在直线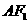 上,
上,
只需求得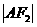 即可; …………………………………8分
即可; …………………………………8分
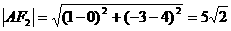 , ……………………10分
, ……………………10分
∴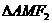 的周长为
的周长为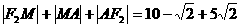
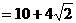 . ……………………………………………12分
. ……………………………………………12分
19、解:(1)证明:∵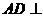 平面
平面 ,
,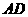 ∥
∥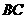 ,
,
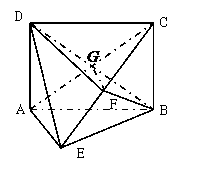 ∴
∴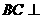 平面
平面 ,则
,则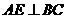 , ……………………2分
, ……………………2分
又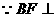 平面
平面 ,则
,则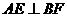
∴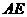 ⊥平面
⊥平面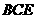 ;…………… 4分
;…………… 4分
(2)由题意可得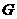 是
是 的中点,连接
的中点,连接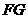
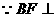 平面
平面 ,则
,则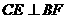 ,
,
而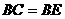 ,∴
,∴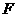 是
是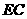 中点
;………6分
中点
;………6分
在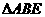 中,
中,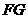 ∥
∥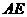 ,∴
,∴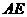 ∥平面
∥平面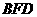 . ……………8分
. ……………8分
(3)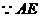 ∥平面
∥平面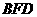 ,∴
,∴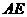 ∥
∥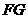 ,
,
而∴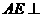 平面
平面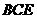 ,∴
,∴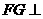 平面
平面
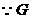 是
是 中点,
中点,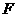 是
是 中点,
中点,
∴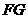 ∥
∥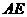 且
且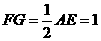 ,
……………………9分
,
……………………9分
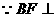 平面
平面 ,∴
,∴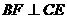 ,
,
∴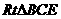 中,
中,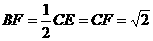 , ………………10分
, ………………10分
∴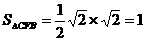 …………………………11分
…………………………11分
∴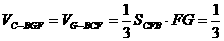 ………………12分
………………12分
18、解:由题意得: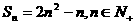 , ……………………1分
, ……………………1分
(1)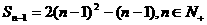 且
且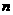 ≥
≥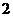 ,可得
,可得
∴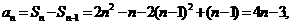 …………3分
…………3分
当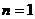 时,
时,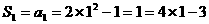
∴数列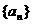 的通项公式为
的通项公式为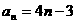 . ………………6分
. ………………6分
(2)由题意过点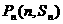 的切线斜率为
的切线斜率为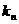 ,则
,则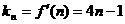
∴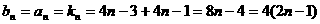 ,……9分
,……9分
∴数列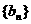 为等差数列,即
为等差数列,即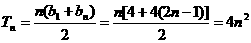
∴数列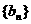 的前
的前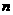 项和为
项和为
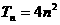 . …………………12分
. …………………12分
17、解: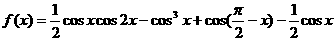
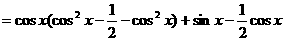
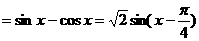 . ………………2分
. ………………2分
(1)当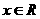 时,
时,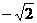 ≤
≤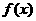 ≤
≤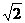 ;
;
∴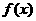 的最大值为
的最大值为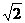 ,最小值为
,最小值为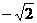 ;……5分
;……5分
(2)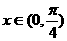 时,
时,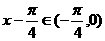 ,
,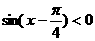
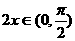 ,
,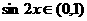 ;
…………7分
;
…………7分
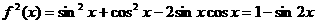 ;
;
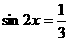 ,则
,则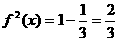 ;……………9分
;……………9分
∵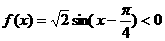
∴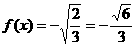 . ………………………12分
. ………………………12分
15、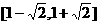 .
16、2
.
.
16、2
.
13、19375+1250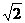 .
14、
.
14、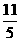 或 1 .
或 1 .
22、(本小题满分14分)
设函数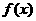 的定义域为
的定义域为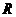 ,当
,当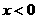 时,
时,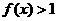 ,且对于任意的实数
,且对于任意的实数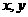 都有
都有
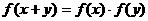 成立,
成立,
(1)求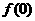 的值,判断并证明函数
的值,判断并证明函数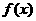 的单调性;
的单调性;
(2)若数列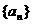 满足
满足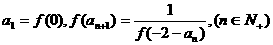 ,求
,求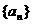 的通项公式;
的通项公式;
(3)如果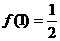 ,
,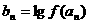 ,求数列
,求数列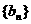 的前
的前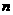 项和
项和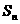 .
.
文科数学试卷答案及评分标准
21、(本小题满分12分)
已知椭圆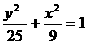 的上、下焦点分别为
的上、下焦点分别为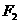 和
和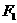 ,点
,点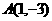 ,
,
(1)在椭圆上有一点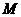 ,使
,使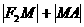 的值最小,求最小值;
的值最小,求最小值;
(2)当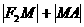 取最小值时,求三角形
取最小值时,求三角形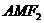 的周长.
的周长.
20、(本小题满分12分)
考察下列式子:
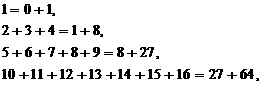
…………………………………………………;
请你做出一般性的猜想,并且证明你猜想的结论。
19、(本小题满分12分)
如图所示,矩形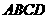 中,
中,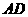 ⊥平面
⊥平面 ,
,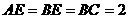 ,
,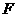 为
为 上的点,且
上的点,且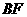 ⊥平面
⊥平面 ,
,
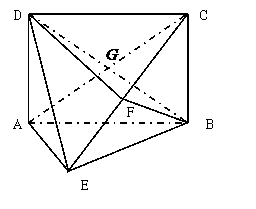
 交
交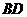 于点
于点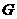 ,
,
(1)求证: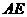 ⊥平面
⊥平面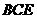 ;
;
(2)求证: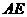 ∥平面
∥平面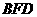 ;
;
(3)求三棱锥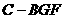 的体积.
的体积.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com