
题目列表(包括答案和解析)
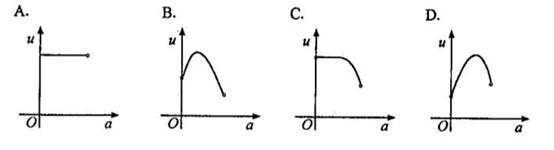
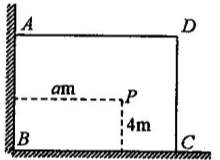
12.如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是am(0<a<12)、4m,不考虑树的粗细,现在想用16m长的篱笆,借助墙角为成一个矩形的花圃ABCD,设此矩形花圃的面积为Sm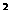 ,S的最大值为f(a),若将这棵树围在花圃内,则函数u=f(a)的图像大致是
,S的最大值为f(a),若将这棵树围在花圃内,则函数u=f(a)的图像大致是
10.已知曲线C:y=2x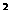 ,点 A(0,-2)及点B(3,a),从点A观察点B,要使实现不被曲线C挡住,则实数a的取值范围是
,点 A(0,-2)及点B(3,a),从点A观察点B,要使实现不被曲线C挡住,则实数a的取值范围是
A.(4,+ ) B.(
) B.(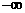 ,4)
C.(10,
,4)
C.(10, )
D.
)
D.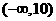
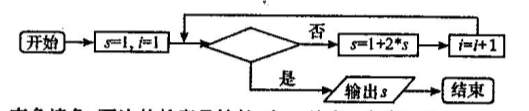
11下图是把二进制数11111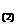 化成十进制数的一个程序框图,判断框内应填入的条件是
化成十进制数的一个程序框图,判断框内应填入的条件是
A.i>5
B.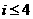 C.i>4
D.i
C.i>4
D.i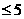
7.已知实数x,y满足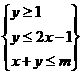 如果目标函数z=x-y的最小值为-1,则实数m等于
如果目标函数z=x-y的最小值为-1,则实数m等于
A.7 B.5 C.4 D.3
8如图在长方体ABCD-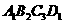 中,三棱锥A
中,三棱锥A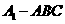 的面是直角三角行的个数为:
的面是直角三角行的个数为:
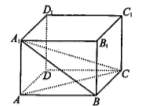
A.1 B.2 C.3 D.4
9已知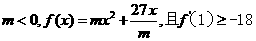 则实数m等于
则实数m等于
A.-9 B.-3 C.3 D.9
6.若
A. 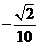 B.
B.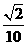 C
C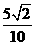 D.
D.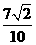
4. 右面程序运行后,输出的值是
右面程序运行后,输出的值是
A.42 B.43
C.44 D.45
5设 A、B、C、D是空间四个不同的点,在下列命题中,不正确的是
A. 若AC与BD共面,则AD与BC 共面
B. 若AC与BD是异面直线,则AD与BC是异面直线
C.
若AB=AC,DB=DC,则AD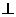 BC
BC
D.
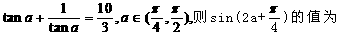 若AB=AC,DB=DC,则AD=BC
若AB=AC,DB=DC,则AD=BC
2.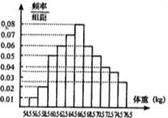 为了了解某校学生的身体发育情况,抽查了该 校100 名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2000名高中男生体重大于70.5公斤的人数为
为了了解某校学生的身体发育情况,抽查了该 校100 名高中男生的体重情况,根据所得数据画出样本的频率分布直方图如图所示,根据此图,估计该校2000名高中男生体重大于70.5公斤的人数为
A.400 B.200
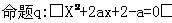
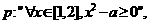 C.128
D.20
C.128
D.20
3已知命题
若命题“q且p”是真命题,则实数a的取值范围是
A.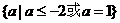 B.
B. 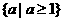
C. 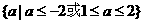 D.
D.
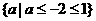
只有一项是符合题目要求的。
1. 化简i(2i-1)=
A-2+i B.2+I C-2+i D.-2-i
21.(本小题满分12分)
已知函数f(x)=lnx-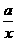 ,
,
(I) 求函数f(x)的单调增区间;
(II)
若函数f(x)在[1,e]上的最小值为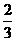 ,求实数a的值。
,求实数a的值。
22(本小题满分14分)
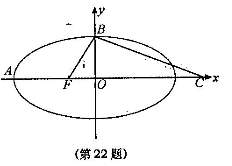 如图,F是团圆
如图,F是团圆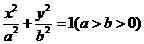 的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为
的一个焦点,A、B是椭圆的两个顶点,椭圆的离心率为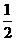 ,点C在X轴上,BC
,点C在X轴上,BC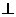 BF,B,C,F三点确定的圆M恰好与直线
BF,B,C,F三点确定的圆M恰好与直线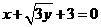 相切。
相切。
(I) 求椭圆的方程;
(II) 过F作一条与两坐标都不垂直的直线l交椭圆于P、Q两点,在x轴上是否存在点N,使得NF恰好为PNQ的内角评分线,若存在,求出点N的坐标,若不存在,请说明理由。
20. (本小题满分12分)
(本小题满分12分)
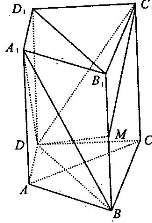
如图所示,在直四棱柱ABCD-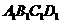 中,DB=BC,DB
中,DB=BC,DB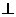 AC,点M是棱BB
AC,点M是棱BB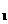 上一点。
上一点。
(I)
求证:B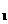 D
D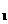
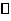 面
面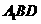 ;
;
(II)
求证:MD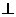 AC;
AC;
(III)
试确定点M的位置,使得平面DMC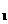
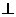 平面
平面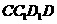
18.(本小题满分12分)
已知数列{a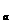 }中,
}中,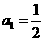 ,点
,点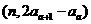 在直线y=x上,其中n=1,2,3….
在直线y=x上,其中n=1,2,3….
(I)
令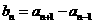 ,求证数列{b
,求证数列{b }是等比数列;
}是等比数列;
(II)
球数列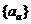 的通项
的通项
19(本小题满分12分)
在甲、乙两个盒子中分别装有标号为1,2,3,4的四个小球,现从甲、乙两个盒子中各取出一个小球,每个小球被取出的可能性相等。
(I) 求取出的两个小球上的标号为相邻整数的概率;
(II) 求取出的两个小球上的标号之间和能被3整除的概率;
(III) 球取出的两个小球上的标号只和大于5的概率
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com