
题目列表(包括答案和解析)
20. (本小题满分12分)

19. (本小题满分12分)

18. (本小题满分12分)
北京时间8月14日中国射箭老将张娟娟在第29届北京奥运会射箭个人决赛中以110:109击败韩国卫冕冠军朴成贤。射箭决赛中,每位选手共射击12箭,已知张娟娟击中10环4次、9环7次、7环1次,朴成贤击中10环4次、9环5次、8环3次。
(1) 若再让两人各自射击3次,张娟娟与朴成贤各恰好两次击中9环的概率哪个大(结果以分数的形式表示)?
(2) 若在让两人各自射击3次,求朴成贤每次都击中9环以上的概率(结果一分数的形式表示)
(理)(3)设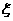 为张娟娟在这次决赛中击中的环数,求
为张娟娟在这次决赛中击中的环数,求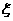 的期望。
的期望。
17.(本小题满分10分)

16.下列两个命题,是否需要在“ ”上加一个条件或结论才能构成真命?如果需要,请填写出一个相应的条件;如果不需要,则在“ ”上划“/”

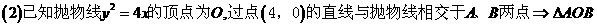
1.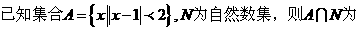
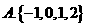
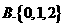
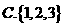
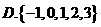

A. 0.5 B.0.7 C. 0.25 D. 0.05
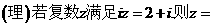
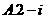
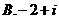
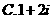
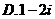

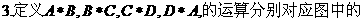 ①②③④,那么图中的⑤⑥所对应的运算结果可能是
①②③④,那么图中的⑤⑥所对应的运算结果可能是
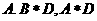
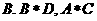
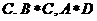
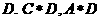
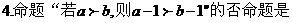
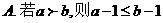
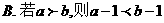
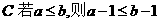
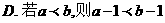
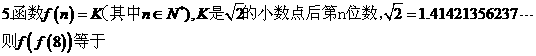
A. 1 B.3 C.4 D.6
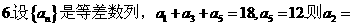
A. 2 B.3 C.4 D.5’
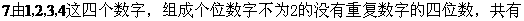
A 8个 B.9个 C.18个 D.19个
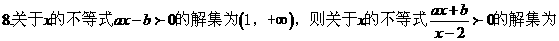
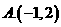
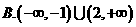
C.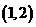
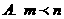
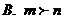



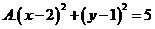
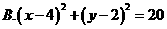
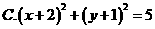
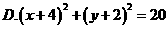
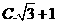 D.2
D.2
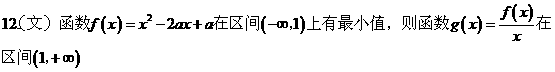 A. 有最小值
B. 有最大值 C. 是减函数
D. 是增函数
A. 有最小值
B. 有最大值 C. 是减函数
D. 是增函数
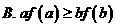
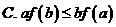
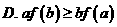
第Ⅱ卷(非选择题 共90分)
(17)(本小题满分12分)
在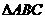 中,
中,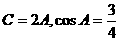
(Ⅰ)求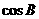 ;
;
(Ⅱ)若·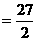 ,求边
,求边 的长。
的长。
(18)(本小题满分12分)
已知函数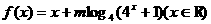 是偶函数。
是偶函数。
(Ⅰ)求 的值;
的值;
(Ⅱ)若方程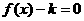 有解,求
有解,求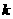 的取值范围。
的取值范围。
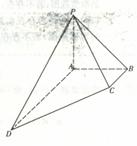
(19)(本小题满分t2分)
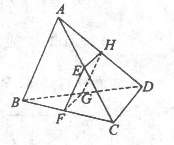
如图,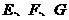 分别是三棱锥
分别是三棱锥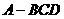 的棱
的棱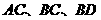 的中点,过三点
的中点,过三点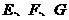 的平面交
的平面交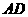 于
于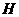 。
。
(Ⅰ)求证:四边形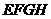 是平行四边形;
是平行四边形;
 (Ⅱ)已知
(Ⅱ)已知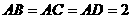 ,
,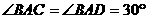 ,试在棱
,试在棱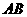 上找一点
上找一点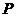 ,使平面
,使平面 平面
平面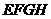 ,并说明理由。
,并说明理由。
(20)(本小题满分12分)
已知函数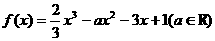
(Ⅰ)若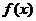 在区间
在区间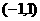 上为减函数,求
上为减函数,求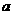 的取值范围;
的取值范围;
(Ⅱ)讨论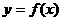 在
在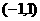 内的极值点的个数。
内的极值点的个数。
(21)(本小题满分14分)
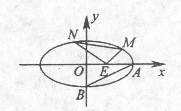 如图,中心在原点,焦点在
如图,中心在原点,焦点在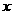 轴上的椭圆的离心率
轴上的椭圆的离心率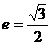 ,
,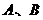 分别是椭圆的长轴、短轴的端点,原点
分别是椭圆的长轴、短轴的端点,原点 到直线
到直线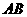 的距离为
的距离为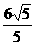 。
。
(Ⅰ)求椭圆的标准方程;
(Ⅱ)已知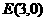 ,设点
,设点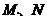 是椭圆上的两个动点,
是椭圆上的两个动点,
满足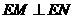 ,求
,求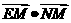 的取值范围.
的取值范围.
(22)(本小题满分14分)
已知数列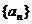 中,
中,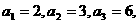 当
当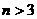 且
且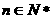 有:
有:
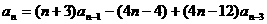 。
。
(Ⅰ)设数列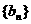 满足
满足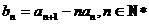 ,证明散列
,证明散列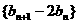 为等比数列,并求数列
为等比数列,并求数列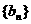 的通项公式;
的通项公式;
(Ⅱ)记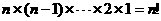 ,规定
,规定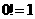 ,求数列
,求数列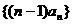 的前
的前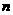 项和
项和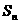 。
。
和平区2008-2009学年度第二学期高三年级
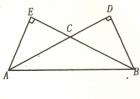
(11)已知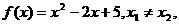 且
且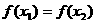 ,则
,则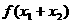 的值为________。
的值为________。
 (12)圆
(12)圆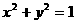 上的点与直线
上的点与直线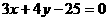 的最小距离为___________________。
的最小距离为___________________。
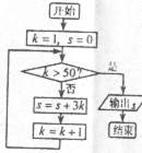
(13)在如右图所示的程序框图中,当程序被执行后,输出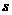 的数值是______。
的数值是______。
(14)在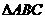 中,
中,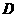 是
是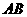 边上一点,若=
边上一点,若=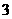 ,
,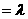
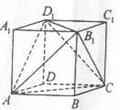
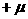 ,则
,则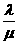 的值为____________。
的值为____________。
(15)如图,将棱长为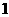 的正方体
的正方体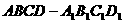 ,截去四
,截去四
个三棱锥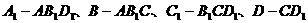 ,
,
 得到的几何体
得到的几何体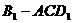 的体积等于___________。
的体积等于___________。
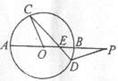
(16)如图,圆 的割线
的割线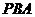 过圆心
过圆心 ,弦
,弦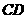 交
交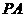 于点
于点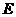 ,
,
且 -
-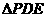 ,
,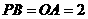 则
则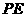 的长等于_______。
的长等于_______。
(1)若复数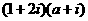 为纯虚数,
为纯虚数,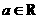 ,则
,则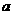 等于
等于
(A)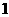 (B)
(B)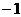
(C)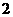 (D)
(D)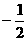
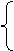
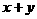 ≥
≥
(2)在平面直角坐标系中,不等式组 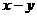 ≥
≥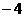 表示的平面区域的面积等于
表示的平面区域的面积等于
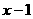 ≤
≤
(A)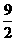 (B)
(B)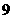
(C)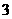 (D)
(D)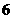
(3)已知命题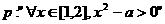 ,命题
,命题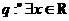 ,使
,使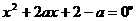 。若命题
。若命题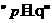 是真命题,则实数
是真命题,则实数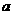 的取值范围是
的取值范围是
(A)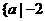 ≤
≤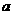 ≤
≤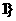 (B)
(B)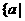
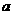 ≥
≥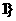
(C) 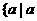 ≤
≤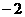 或
或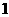 ≤
≤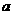 ≤
≤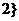 (D)
(D)
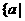
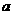 ≤
≤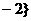
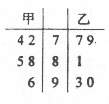 (4)甲、乙两名同学在
(4)甲、乙两名同学在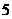 次数学测验中的成绩统计如右面的茎叶图所示,
次数学测验中的成绩统计如右面的茎叶图所示,
则甲、乙两人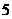 次数学测验的平均成绩依次为
次数学测验的平均成绩依次为
(A)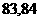 (B)
(B)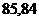
(C)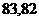 (D)
(D)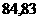
(5)已知数列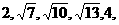 …,则
…,则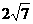 是该数列的
是该数列的
(A)第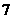 项 (B)第
项 (B)第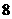 项
项
(C)第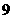 项 (D)第
项 (D)第 项
项
(6)若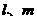 表示互不重合的两条直线,
表示互不重合的两条直线,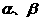 表示互不重合的两个平面,则
表示互不重合的两个平面,则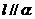 的一个充分条件是
的一个充分条件是
(A)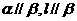 (B)
(B)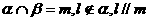
(C)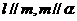 (D)
(D)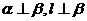
(7)若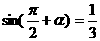 则
则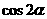 等于
等于
(A) (B)
(B)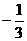
(C)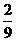 (D)
(D)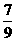
(8)在数字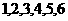 中随机地抽取两个数字,它们的和大于
中随机地抽取两个数字,它们的和大于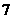 的概率是
的概率是
(A)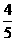 (B)
(B)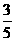
(C)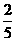 (D)
(D)
(9)双曲线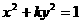 的离心率
的离心率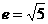 则
则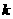 为
为
(A)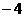 (B)
(B)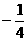
(C)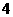 (D)
(D)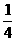
(10)若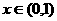 ,则下列结论正确的是
,则下列结论正确的是
(A)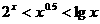 (B)
(B)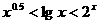
(C)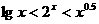 (D)
(D)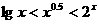
第Ⅱ卷
22.(本小题满分14分)
设等比数列{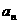 }的前
}的前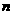 项和
项和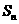 ,首项
,首项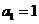 ,公比
,公比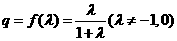 .
.
(Ⅰ)证明: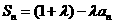 ;
;
(Ⅱ)若数列{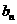 }满足
}满足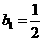 ,
,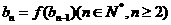 ,求数列{
,求数列{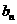 }的通项公式;
}的通项公式;
(Ⅲ)若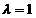 ,记
,记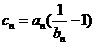 ,数列{
,数列{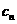 }的前项和为
}的前项和为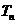 ,求证:当
,求证:当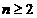 时,
时,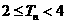 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com