
题目列表(包括答案和解析)
7.一文艺演出中,需给舞台上方安装一排彩灯共15只,以不同的点亮方式增加舞台效果,要求设计者按照“每次点亮时,必须有6只是关的,且相邻的灯不能同时被关掉,两端的灯必须点亮”的要求进行设计,那么不同点亮方式的种数是( )
A.28 B.84 C.180 D.360
6.设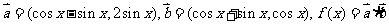 ,将函数
,将函数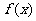 的图像按向量
的图像按向量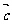 平移而得到函数g(x)=
平移而得到函数g(x)=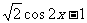 ,则
,则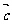 可以为( )
可以为( )
A.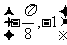 B.
B.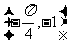 C.
C.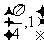 D.
D.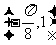
5.等差数列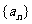 的公差为d,前n项和为
的公差为d,前n项和为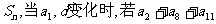 是一个定值,那么下列各数中也为定值的是( ) A.S13; B.S15 C.S7 D.S8
是一个定值,那么下列各数中也为定值的是( ) A.S13; B.S15 C.S7 D.S8
4.在正三棱锥 中,D、E分别是AB、BC的中点,有下列四个论断:
中,D、E分别是AB、BC的中点,有下列四个论断:
①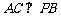 ; ②
; ②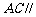 平面PDE;③
平面PDE;③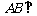 平面PDE; ④平面
平面PDE; ④平面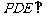 平面ABC.
平面ABC.
其中正确的个数为( ) A.1个 B.2个 C.3个 D.4个
3.若不等式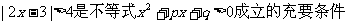 ,则
,则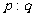 等于( )
等于( )
A.12 : 7 B.7 : 12 C.(-12): 7 D.(-3): 4
2.设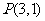 为函数
为函数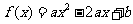 (
(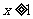 )的图像与其反函数
)的图像与其反函数 的图像的一个交点,则( )
的图像的一个交点,则( )
A.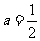 ,
,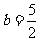 B.
B.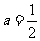 ,
,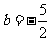
C.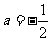 ,
,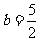 D.
D.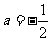 ,
,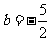
1.已知集合P={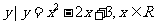 }, Q={
}, Q={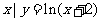 },则
},则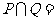 ( )
( )
A.R B.(-2,+ ) C.
) C.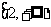 D.
D.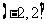
20.已知以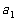 为首项的数列
为首项的数列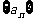 满足:
满足: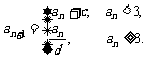
(1)当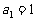 ,
,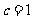 ,
,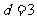 时,求数列
时,求数列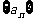 的通项公式;
的通项公式;
(2)当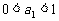 ,
,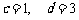 时,试用
时,试用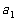 表示数列
表示数列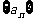 前100项的和
前100项的和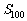 ;
;
(3)当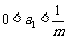 (
(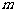 是正整数),
是正整数),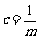 ,正整数
,正整数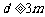 时,求证:数列
时,求证:数列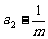 ,
,
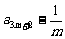 ,
,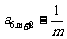 ,
,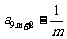 成等比数列当且仅当
成等比数列当且仅当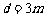 .
.
19.已知数列{an}、{bn}满足:a1=λ,an+1=an+n-4,bn=(-1)n(an-3n+21),其中λ为实数,n为正整数.
(1)对任意实数λ,证明数列{an}不是等比数列;
(2)对于给定的实数λ,试求数列{bn}的前n项和Sn;
(3)设0<a<b,是否存在实数λ,使得对任意正整数n,都有a<Sn<b成立? 若存在,求λ的取值范围;若不存在,说明理由.
18.已知正项数列{ an }满足Sn+Sn-1=ta+2,(n≥2,t>0),a1=1,其中Sn是数列{ an }的前n项和.
(1)求通项an;
(2)记数列{}的前n项和为Tn,若Tn<2对所有的n∈N+恒成立.求证:0<t≤1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com