
题目列表(包括答案和解析)
22.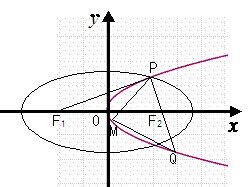 如图,设抛物线
如图,设抛物线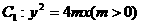 的准线与
的准线与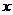 轴交于
轴交于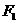 ,焦点为
,焦点为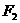 .以
.以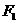 ,
,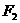 为焦点,离心率
为焦点,离心率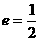 的椭圆
的椭圆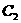 与抛物线
与抛物线 在
在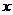 轴上方的交点为
轴上方的交点为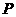 ,延长
,延长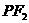 交抛物线于点
交抛物线于点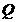 ,
,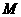 是抛物线
是抛物线 上一动点,且
上一动点,且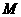 在
在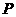 与
与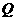 之间运动.
之间运动.
(1)当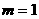 时,求椭圆
时,求椭圆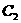 的方程;
的方程;
(2)当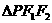 的边长恰好是三个连续的自然数时,求
的边长恰好是三个连续的自然数时,求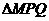 面积的最大值.
面积的最大值.
21.(1) m=0,且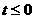 时交点为(0,0);
时交点为(0,0); 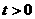 时交点为(
时交点为(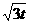 ,0)、(-
,0)、(-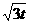 ,0)
,0)
 (2)
(2)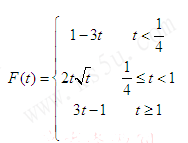
21.函数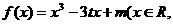
 和
和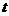 为实常数)是奇函数.
为实常数)是奇函数.
(1)求实数 的值和函数
的值和函数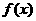 的图象与
的图象与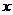 轴的交点坐标.
轴的交点坐标.
(2)设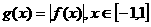 ,求
,求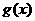 的最大值
的最大值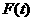 .
.
2.山西一模
22. (Ⅰ)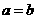 (Ⅱ)
(Ⅱ) (Ⅲ)
(Ⅲ)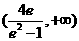
22.(本小题满分14分)已知函数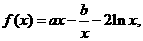 且
且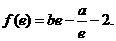
(Ⅰ)求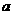 与
与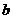 的关系式; (Ⅱ)若
的关系式; (Ⅱ)若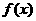 在定义域内为单调函数,求
在定义域内为单调函数,求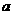 的取值范围;
的取值范围;
(Ⅲ)设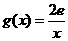 ,若在
,若在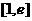 上至少存在一点
上至少存在一点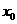 ,使得
,使得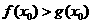 成立,求
成立,求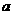 的取值范围。
的取值范围。
21. (Ⅰ)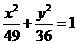 和
和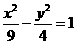 (Ⅱ)
(Ⅱ)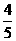
20. (Ⅰ)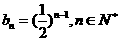
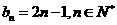 (Ⅱ)
(Ⅱ)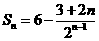

2. 曲靖一中

22. 解:(1)令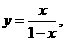 解得
解得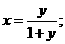 由
由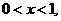 解得
解得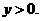
∴函数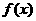 的反函数
的反函数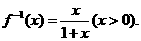
则错误!不能通过编辑域代码创建对象。
得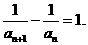
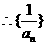 是以2为首项,1为公差的等差数列,故
是以2为首项,1为公差的等差数列,故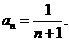 …………4分
…………4分
(2)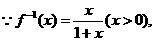
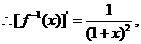
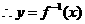 在点
在点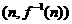 处的切线方程为
处的切线方程为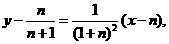
令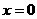 得
得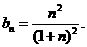
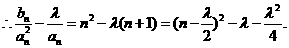
 仅当
仅当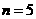 时取得最小值,
时取得最小值,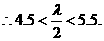 ∴
∴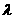 的取值范围为
的取值范围为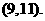 ………8分
………8分
(3)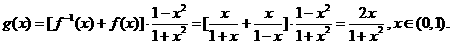
所以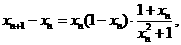 又因
又因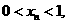 则
则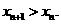
显然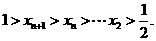 …………………………10分
…………………………10分
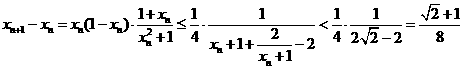
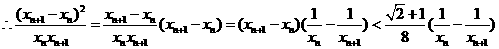
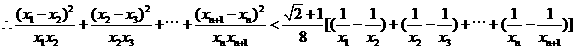
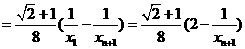 …………………………12分
…………………………12分
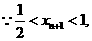
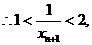
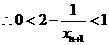
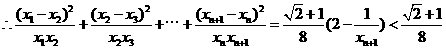 .……………14分
.……………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com